سوالات ۱۱ تا ۱۳
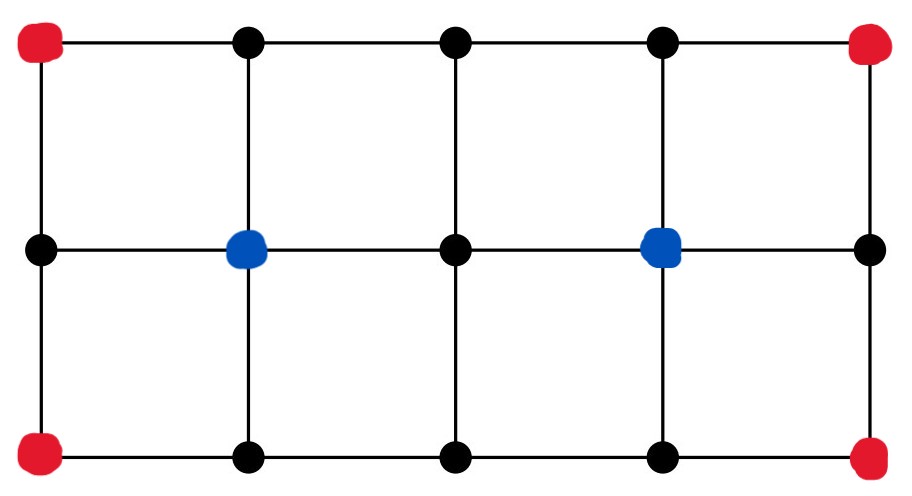
شبکە ی ۵ × ۳ زیر را در نظر بگیرید. به دو نقطه مجاور میگوییم اگر با یک پارە خط مستقیم (بدون عبور از
نقطە ای دیگر)، به هم وصل شده باشند.

با توجه به توضیحات بالا به ۳ سوال زیر پاسخ دهید.
سوال ۱۱
حداقل چند نقطه را باید علامت بزنیم، به طوری که هر نقطە ی بی علامت با حداقل یک نقطە ی علامت دار، مجاور باشد؟
- ۳
- ۵
- ۴
- ۶
- ۷
راهنمایی
میگوییم یک نقطه پوشش داده شده است، اگر خودش یا حداقل یکی از نقاط مجاورش علامت زده شده باشند.
برای اینکه نشان دهیم جواب برابر با $k$ است، باید دو چیز را نشان دهیم:
- راهی وجود دارد که با علامت زدن $k$ نقطه تمام نقاط را پوشش دهیم.
- هیچ راهی وجود ندارد که با علامت زدن کمتر از $k$ نقطه بتوانیم تمام نقاط را پوشش دهیم.
سعی کنید یک کران بالا و یک کران پایین برای جواب پیدا کنید و کرانهای بالا و پایین را به هم نزدیک کنید.
راهنمایی
برای پیدا کردن یک کران پایین، به این دقت کنید که با علامت زدن هر نقطه، حداکثر چند نقطه پوشش داده میشوند؟
با توجه به این مقدار و اینکه این شبکه از $15$ نقطه تشکیل شده است، برای اینکه همهی نقطهها پوشش داده شوند به حداقل چند نقطهی علامتزده نیاز داریم؟
راهنمایی
سعی کنید مثالی برای پوشش دادن همهی نقطهها با علامت زدن $5$ نقطه پیدا کنید.
راهنمایی
طبق دو راهنمایی قبل میدانیم جواب از $3$ کمتر و از $5$ بیشتر نیست.
تلاش کنید مثالی برای پوشش دادن همهی نقاط با علامت زدن دقیقاً $3$ نقطه پیدا کنید، یا ثابت کنید این کار امکانپذیر نیست.
راهنمایی
مثالی برای پوشش دادن همهی نقاط با علامت زدن $4$ نقطه پیدا کنید.
سوال ۱۲
پاسخ سوال قبل را $k$ نقطه در نظر بگیرید. به چند روش میتوانیم $k$ نقطه را علامت بزنیم، به طوری که هر نقطە ی بی علامت با حداقل یک نقطە ی علامت دار، مجاور باشد؟
- ۱
- ۴
- ۵
- ۳
- ۲
راهنمایی
میخواهیم تعداد روشهای پوشش دادن همهی نقاط، با علامت زدن دقیقاً $4$ نقطه را بشماریم.
نشان دهید اگر بخواهیم $4$ نقطه را علامت بزنیم به طوری که همهی نقاط پوشش داده شوند، هیچ نقطهی گوشهای علامت زده نمیشود.
راهنمایی
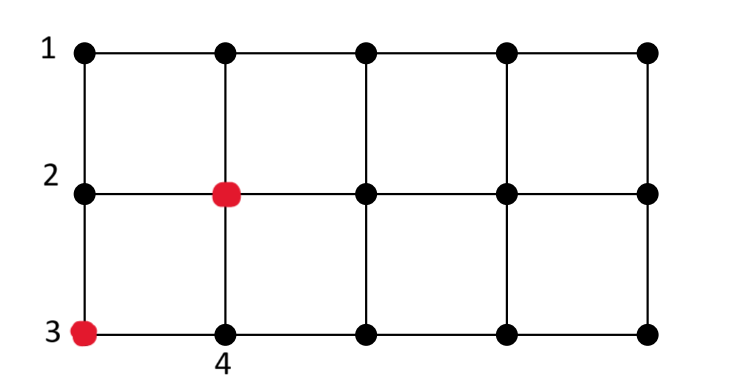
بدون از دست دادن کلیت مسئله، فرض میکنیم نقطهی شماره 1 را علامت زدهایم؛ در ا ینصورت نقاط سبز پوشش داده میشوند.
 برای پوشش دادن نقطهی 3 باید یکی از نقاط 2، 3 یا 4 علامت زده شود. این حالتها را بررسی میکنیم:
برای پوشش دادن نقطهی 3 باید یکی از نقاط 2، 3 یا 4 علامت زده شود. این حالتها را بررسی میکنیم:
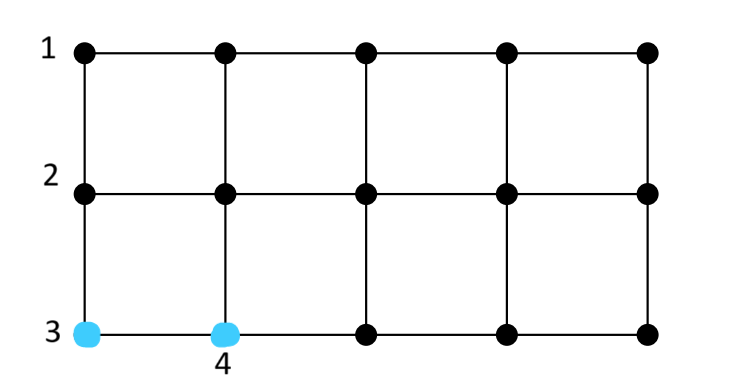
- نقطهی شماره 2 علامت زده شود: در اینصورت نقاط قرمز پوشش داده میشوند.(نقاط شماره 1 و 2 قبلاً پوشش داده شدهاند)
- نقطهی شماره 3 علامت زده شود: در اینصورت نقاط آبی پوشش داده میشوند.(نقطهی شماره 2 قبلاً پوشش داده شده است)
- نقطهی شماره 4 علامت زده شود: در اینصورت نقاط بنفش پوشش داده میشوند.
 نقاط آبی و قرمز زیرمجموعهی نقاط بنفش هستند؛ در نتیجه، اگر روشی برای پوشش دادن همهی نقاط با علامت زدن $4$ خانه وجود داشته باشد، به طوری که علاوه بر نقطهی شماره 1 یکی از نقاط شماره 2 یا 3 هم علامت زده شده باشد، روشی برای این کار وجود دارد به طوری که نقاط شماره 1 و 4 علامت زده شده باشند و نقاط شماره 2 و 3 علامت زده نشده باشند.
نقاط آبی و قرمز زیرمجموعهی نقاط بنفش هستند؛ در نتیجه، اگر روشی برای پوشش دادن همهی نقاط با علامت زدن $4$ خانه وجود داشته باشد، به طوری که علاوه بر نقطهی شماره 1 یکی از نقاط شماره 2 یا 3 هم علامت زده شده باشد، روشی برای این کار وجود دارد به طوری که نقاط شماره 1 و 4 علامت زده شده باشند و نقاط شماره 2 و 3 علامت زده نشده باشند.
نشان دهید هیچ راهی وجود ندارد که با علامت زدن نقاط شمارهی 1 و 4 و دو نقطهی دیگر، همهی نقاط پوشش داده شوند. به این ترتیب ثابت میشود که اگر بخواهیم با علامت زدن $4$ نقطه همهی نقاط را پوشش دهیم، نباید هیچ گوشهای را علامت بزنیم.
راهنمایی
سوال ۱۳
حداقل چند نقطه را باید علامت بزنیم، به طوری که هر نقطە ی بی علامت با حداقل دو نقطە ی علامت دار، مجاور باشد؟
- ۸
- ۷
- ۹
- ۵
- ۶
راهنمایی
میگوییم یک نقطه پوشش داده شده است، اگر خودش یا حداقل دوتا از نقاط مجاورش علامت زده شده باشند.
سعی کنید نشان دهید این کار با علامت زدن $6$ نقطه امکانپذیر نیست.
راهنمایی
با حالت بندی روی تعداد نقطههای گوشهی علامتدار، تلاش کنید حکم راهنمایی قبل را ثابت کنید.
راهنمایی
اگر یک نقطه از گوشهی شبکه علامت زده نشده باشد، باید هردو نقطهی مجاورش علامت داشته باشند.
راهنمایی
نشان دهید اگر صفر یا یکی از نقطههای گوشهی شبکه علامت زده شده باشند، نمیتوانیم با علامت زدن $6$ نقطه همهی نقاط را پوشش دهیم.
راهنمایی
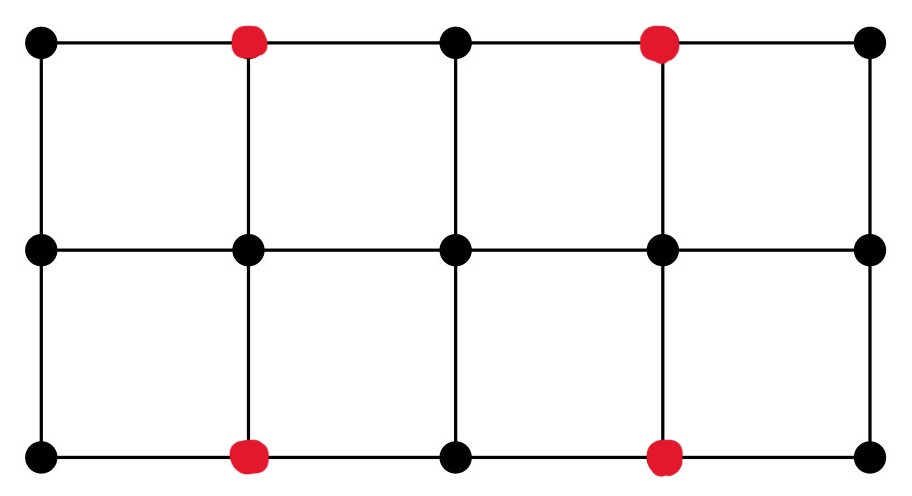
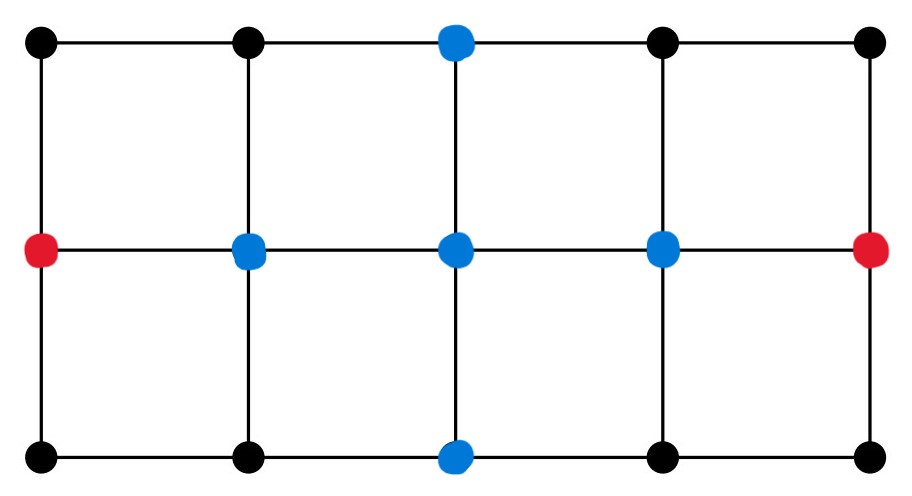
اگر $3$تا از نقطههای گوشهی شبکه علامت زده شده باشند، (بدون از دست دادن کلیت مسئله، فرض کنید نقاط قرمز شکل زیر علامت زده شدهاند و نقطهی سبز علامت زده نشدهاست)، با بررسی شرایط پوشش دادن نقطهی آبی، نشان دهید نمیتوان با علامت زدن $6$ نقطه همهی نقاط را پوشش داد.
 با روشهایی که تا اینجا به کار بردیم، به راحتی میتوان همین حکم را برای حالتی که دوتا از نقاط گوشهی شبکه علامت زده شده باشند نیز ثابت کرد.
با روشهایی که تا اینجا به کار بردیم، به راحتی میتوان همین حکم را برای حالتی که دوتا از نقاط گوشهی شبکه علامت زده شده باشند نیز ثابت کرد.
| ▸ سوال قبل | سوال بعد ◂ |