سوال ۵
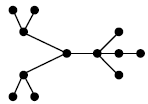 شکل روبهرو ۱۲ رأس دارد که ۱۱ زوج آن با پارهخطهایی بههم وصل شدهاند.
میخواهیم هرکدام از رأسها را با یکی از سه رنگ موجود رنگ کنیم به طوری که هیچ ۲ رأس متصل بههم، یکرنگ نشوند. بهچند طریق این کار ممکن است؟
شکل روبهرو ۱۲ رأس دارد که ۱۱ زوج آن با پارهخطهایی بههم وصل شدهاند.
میخواهیم هرکدام از رأسها را با یکی از سه رنگ موجود رنگ کنیم به طوری که هیچ ۲ رأس متصل بههم، یکرنگ نشوند. بهچند طریق این کار ممکن است؟
- کمتر از ۱۰۰۰ طریق
- بین ۱۰۰۰ و ۳۰۰۰ طریق
- بین ۳۰۰۰ و ۶۰۰۰ طریق
- بین ۶۰۰۰ و ۲۰۰۰۰ طریق
- بین ۲۰۰۰۰ و ۱۰۰۰۰۰ طریق
پاسخ
گزینه (۴) درست است.
یکی از رئوس از درجهی واحد راانتخاب و آن را با یکی از سه رنگ موجود رنگ میکنیم. راس متصل به آن٬ سپس راس متصل به دومی و … را به دو طریق میتوانیم رنگ کنیم٬ بنابراین تعداد روشهای مطلوب برابر $3\times2^{11}$ یعنی ۶۱۴۴ خواهد شد.
| ▸ سوال قبل | سوال بعد ◂ |