سوال ۴
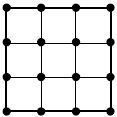شکل روبهرو از ۲۴ پارهخط و ۱۶ نقطه تشکیل شده است. میبینید که در بیشترین حالت برای رفتن از یک نقطه بهیک نقطه دیگر باید از حداقل ۶ پارهخط بگذریم. میخواهیم از مجموع ۱۸ قطر مربعهای کوچک ۲ تا را رسم کنیم تا در بیشترین حالت با پیمایش ۵ پارهخط بتوان از هر نقطه به هر نقطهی دیگر رسید. به چند حالت میتوان این کار را انجام داد؟
- صفر
- ۱
- ۹
- ۳۶
- ۸۱
پاسخ
گزینه (۵) درست است.
هر مربع واحد یک قطر اصلی و یک قطر فرعی و کل شبکه ۹ قطر اصلی و ۹ قطر فرعی دارد که برای رسیدن به منظور لازم است یک قطر اصلی و یک قطر فرعی رسم شود. انتخاب این دو قطر به $\binom{9}{1} \times \binom{9}{1}$؛ یعنی ۸۱ طریق ممکن است.
| ▸ سوال قبل | سوال بعد ◂ |