سوال ۲۲
یک مکعب مشبک $2 \times 2 \times 2$ از ۸ «ریزمکعب» به ابعاد واحد تشکیل شده است. داخل هر ریزمکعب یک رقم صفر یا یک مینویسیم. وجههای این ریزمکعبها که بر روی سطح مکعب قرار دارند را «وجه خارجی» مینامیم. یک وجه خارجیِ ریزمکعبی بهنام $A$ را در نظر میگیریم. به این وجه یک عدد ۲ رقمیِ دودویی نسبت میدهیم. رقم با ارزشتر این عدد رقم نوشتهشدهی داخل ریزمکعب $A$ و رقم دیگر آن رقم داخل ریز مکعب پشت $A$ (نسبت به وجه خارجی مورد نظر) است. این کار را برای همه وجههای خارجی انجام میدهیم. بنابراین روی هر سطح مکعب ۴ عدد دودویی با مقدار بین ۰ تا ۳ دیده میشود. به چند طریق میتوان عددهای داخل ریزمکعبها را تعیین کرد بهگونهای که روی هرکدام از سطحهای مکعب، ۴ عدد متمایز قرار بگیرند؟
- ۰
- ۲
- ۴
- ۸
- ۱۶
پاسخ
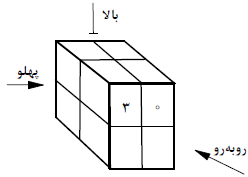
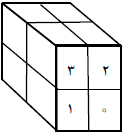
فرض میکنیم اعداد ۰ و ۳ از وجه «روبهرو» مطابق شکل مقابل٬ پهلوی هم باشند در این صورت هر دو عدد نوشته شده در خانههای بالای وجه «پهلو» برابر ۲ خواهد بود که مطلوب نیست. اما اگر اعداد ۰ و ۳ از وجه «روبهرو» مطابق شکل زیر پهلوی هم نباشند در این صورت آنگاه اعداد موجود در ستون اول وجه «پهلو» هر دو برابر ۲ خواهد شد که باز مطلوب نیست. بنابراین هرگز حالت خواسته شده بهدست نمیآید.
| ▸ سوال قبل | سوال بعد ◂ |