ببعی یک جایگشت از اعداد ۰ تا$ ۲^n-1$ را روی تخته‌یادداشت کرده است. گاوی بعد از دیدن دنباله‌ی ببعی، تصمیم گرفت تا تخته را تغییر دهد. گاوی یک درخت دودویی کامل کشید (درختی که در آن هر راس یا برگ است و یا دقیقا دو فرزند دارد) . سپس روی برگ $i$-ام درخت، عدد $i$-ام از جایگشت ببعی را یادداشت کرد و بعد از آن جایگشت ببعی را از روی تخته پاک کرد. ببعی بعد از دیدن درخت گاوی، روی هر راس غیر برگ درخت، یک عدد نوشت، به طوری که عدد نوشته شده روی هر راس، برابر با بیشترین عدد یادداشت شده بر روی دو فرزندش باشد. سپس ببعی مجموع همه‌ی اعداد یادداشت شده روی راس‌های درخت را محاسبه کرد و آن را $M$ نامید.

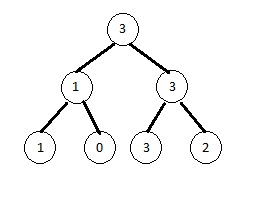
به عنوان مثال اگر $n$برابر ۲ و جایگشت ببعی برابر ۱،۰،۳،۲ باشد، آنگاه درخت گاوی به شکل زیر در می‌آید:

تمام پاسخ‌های ارائه شده در این سوال با فرض $\Delta = 26003$ محاسبه شده‌اند.

$1$- الف (۱۱ نمره) : اگر $n$ برابر با ۳ باشد و بیشترین مقدار و کمترین مقدار ممکن برای $M$ را $m_۱$ و $m_۲$ بنامیم، باقیمانده‌ی تقسیم $(m_۱*m_۲)^۲$ بر $\Delta$ چند است؟

$1$- ب (۱۱ نمره) : اگر $n$ برابر با ۱۲ باشد و بیشترین مقدار و کمترین مقدار ممکن برای $M$ را $m_۱$ و $m_۲$ بنامیم، باقیمانده‌ی تقسیم$(m_۱*m_۲)^۲$ بر $\Delta$ چند است؟

$1$- ج (۱۱ نمره) : اگر $n$ برابر با $۱۰^۶$ باشد و بیشترین مقدار و کمترین مقدار ممکن برای $M$ را $m_۱$ و $m_۲$ بنامیم، باقیمانده‌ی تقسیم $(m_۱*m_۲)^۲$ بر $\Delta$ چند است؟