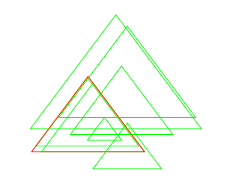
Triangles
یک مثلث شیطانی مثلثی است که مختصات رئوس آن به صورت $(x-3\times k,y)$ ،$(x+3\times k,y)$ و $(x,y+4 \times k)$ که $k$ عددی حقیقی و مثبت است هستند.
به شما مختصات $n$ مثلث شیطانی داده شده است، شما باید کوچکترین مثلث شیطانی را بیابید که حداقل $m$ تا از مثلثهای داده شده در آن قرار بگیرند.
ورودی
- در سطر اول ورودی دو عدد $n$ و $m$ آمده است.
- در هر یک از $n$ سطر بعدی ۳ عدد $x_i$ و $y_i$ و $k_i$ آمده است کهیک مثلث شیطانی را مشخص میکند. تمام اعداد ورودی طبیعی هستند.
- $1 \leq m < n \leq 3000$
- $0 \leq x_i,y_i,k_i \leq 10^7$
- در حداقل ۳۰ درصد تست ها $n$ کمتر یا مساوی ۱۰۰ است
خروجی
فرض کنید مساحت کوچکترین مثلث شیطانی که حداقل $m$ مثلث را دربر دارد برابر با $12.r^2$ باشد. در تنها سطر خروجی عدد $r$ را با دقیقاْ دو رقم اعشار چاپ کنید.
برای چاپ کردن عدد با دقیقاْ دو رقم اعشار میتوانید از دستورات زیر استفاده کنید:
cout<<fixed; cout.precision(2); cout<<result<<endl;
محدودیتها
- محدودیت زمان: ۱ ثانیه
- محدودیت حافظه: ۲۵۶ مگابایت
ورودی و خروجی نمونه
| ورودی نمونه | خروجی نمونه |
|---|---|
| 7 3 5 6 1 8 7 3 7 8 5 3 4 3 2 5 3 9 10 4 9 1 2 | 3.29 |
توضیحات
شکل زیر وضعیت مثلثهای شیطانی را نمایش میدهد. مثلث بهینهای که حداقل ۳ مثلث درون آن قرار میگیرند در شکل با رنگ قرمز نشان داده شده است.
| ▸ سوال قبل | سوال بعد ◂ |