Coloring
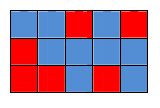
سام و خواهرش سارا یک میز $n \times m$ خانهای دارند. آنها میخواهند تمام خانههای میز را با دو رنگ قرمز و آبی رنگ کنند. طبق یک باور شخصی، آنها میخواهند رنگآمیزی طوری باشد که در پایان، هر مربع $2 \times 2$ از میز تعدادی فردی خانهی قرمز داشته باشد (یعنی یا یکی یا سه تا). بهعنوان مثال، یک رنگآمیزی معتبر یک جدول $5 \times 3$ در شکل زیر نمایش داده شده است.
متأسفانه، شب گذشته، یک غریبه تعدادی از خانههای میز را با قرمز و تعداد دیگری از خانهها را با آبی رنگ کرده است! سام و سارا اکنون میخواهند بدانند آیا میشود سایر خانههای میز را طوری رنگ کرد که در نهایت، رنگآمیزی کل میز مطابق با خواستِ باورشان باشد یا نه؟ و اگر این امر امکانپذیر است، به چند روش میتوان خانههای باقیمانده را طوری رنگ کرد که در هیچ مربع $2 \times 2$ ای، زوج تا خانهی قرمز یافت نشود.
ورودی
- خط آغازین ورودی شامل ۳ عدد صحیح $n, m$ و k میشود که به ترتیب تعداد سطرها، تعداد ستونها و تعداد خانههای «رنگشده در ابتدا» را نشان میدهد.
- سپس $k$ سطر بعدی ورودی شامل مشخصات این خانههای رنگ شده است. خط $i$اُم این بخش سه عدد صحیح $x_i$ ،$y_i$ و $c_i$ را در بردارد که $x_i$ و $y_i$ شماره سطر و ستون $i$اُمین خانهی رنگ شده در ابتدا و $c_i$ رنگِ آن خانه را مشخص میکنند. اگر این خانه به رنگ قرمز رنگ شده باشد، $c_i$ برابر با یک و در غیر این صورت اگر با رنگ آبی رنگ شده باشد، $c_i$ برابر با صفر است.
- تضمین میشود که $k$ خانهی ورودی مکانهای متفاوتی با هم دارند.
- تضمین میشود که در توصیف هر یک از خانههای رنگ شده در ابتدا، $1 \leq x_i \leq n$ و $1 \leq y_i \leq m$.
- در تمامی تستها $2 \leq n, m \leq 10^5$ و $0\leq k \leq 10^5$ است.
- در ۲۰ درصد تستها $n, m \leq 5$ و $k \leq 5$ میباشد.
- در ۵۰ درصد تستها $n, m \leq 500$ و $k \leq 25$ میباشد.
خروجی
در یک سطر تعداد راههای رنگآمیزی میز (که آن را $W$ مینامیم) به پیمانهی $10^9$ را بنویسید. یعنی اگر $W$ مساوی یا بیشتر از $10^9$ است، باقیماندهی تقسیم آن بر $10^9$ را بنویسید.
محدودیتها
- محدودیت زمان: ۱ ثانیه
- محدودیت حافظه: ۶۴ مگابایت
ورودی و خروجی نمونه
| ورودی نمونه | خروجی نمونه |
|---|---|
| 3 4 3 2 2 1 1 2 0 2 3 1 | 8 |
| ▸ سوال قبل | سوال بعد ◂ |