هابیل و قابیل با هم یک بازی عجیب می‌کنند. آن‌ها ابتدا $n$ نقطه روی صفحه رسم میکنند و نقطه‌ها را طوری با $n$ خط (نه لزوماً راست) به هم وصل می‌کنند که هیچ دو خط هم‌دیگر را قطع نکنند (مگر در سرهایشان) و یک دور به وجود آید که از همه‌ی نقاط دقیقاً یک‌ بار عبور کند. شکل رو‌به‌رو مثالی را برای $n= ۱۰$ نشان می‌دهد.

هابیل بازی را شروع می‌کند. هر بازی‌کن در نوبت خودش باید یکی از دو حرکت زیر را انجام دهد:

• یکی از ناحیه‌های صفحه را که توسط خطوط رسم شده در بازی به وجود آمده٬ به طور کامل رنگ کند. این ناحیه نباید قبلاً رنگ شده باشد. می‌توان ناحیه‌ی بیرونی (ناحیه‌ای که مساحت نامتناهی دارد) را هم انتخاب و رنگ کرد.
• دو نقطه که تاکنون با خطی به هم وصل نشده‌اند را با یک خط (نه لزوماً راست) به هم وصل کند٬ به شرطی که این خط جدید از ناحیه‌های رنگ‌شده عبور نکند و با هیچ خط و نقطه‌ی دیگری برخورد نکند.

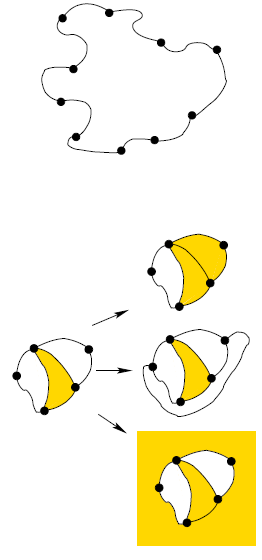
شکل مقابل حرکت‌هایی قابل‌قبول را برای صحنه‌ای از بازی نشان می‌دهد.

کسی که نتواند حرکتی انجام دهد بازنده‌ی بازی است.

برای چه $n$هایی٬ قابیل می‌تواند طوری بازی کند که حتماً برنده‌ی بازی شود؟ ادعای خود را اثبات کنید.