در این مسئله نیاز به موجودی به نام «گراف» داریم؛ ولی فقط به شکل آن نه به مفاهیم نظریه‌ی گراف. گراف شکلی است شامل تعدادی «رأس» که با علامت ● نشان داده می‌شوند و تعدادی یال بین برخی از رأس ها که با خطوط بین آن یال‌ها نشان داده می‌شوند. هر یال دقیقا دو راس را به هم وصل می‌کند که به آن رأس ها رئوس مجاور می‌گوییم.

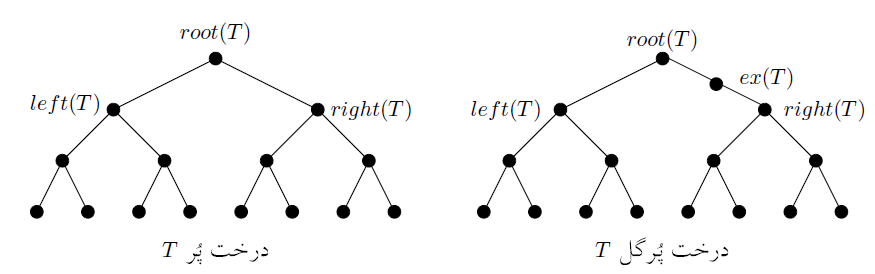
درخت پُرِ$ T$ گرافی است با $2^n - 1$ رأس که‌یک رأس آن ریشه است که$ root(T)$ خوانده می‌شود.$ root(T)$ دو رأس مجاور دارد به نام‌های $left(T)$ و $right(T)$ که هر کدام ریشه‌ی درخت پُری با $2^{n-1}-1$ رأس هستند. اگر یک رأس بین ریشه و یکی از دو فرزند درخت پُرِ $T$ اضافه کنیم، درختی با $2^n$ رأس به دست می‌آید که آن را «پُر گل» و رأس اضافه را $ex(T)$ می‌نامیم. شکل زیر یک درخت پر با ۱۵ رأس و یک درخت پر گل با ۱۶ رأس را نشان می‌دهد.

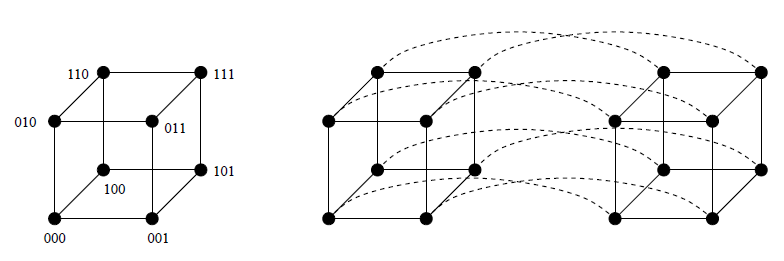
فوق مکعب از درجه‌ی $n$ هم گرافی است با $2^n$ راس، که اگر هر راس آن را با یک عدد $n$ رقمی متمایز در مبنای ۲ نشان دهیم، هر رأس $a_1 a_2 … a_n$ (که $a_i$ یا صفر است و یا ۱) به $n$ رأس دیگر وصل است. دو رأس به هم متصل‌اند اگر نمایش دودویی آن دو دقیقاً در یک رقم اختلاف داشته باشد. می‌توان دید که اگر دو فوق مکعب از درجه‌ی $n$ را بگیریم و بین هر دو رأس از هر دو فوق مکعب با نمایش بیتی یکسان یک یال اضافه کنیم، یک فوق مکعب از درجه‌ی $n+1$ به دست می‌آید. شکل زیر یک فوق مکعب از درجه‌ی ۳ و فوق مکعب درجه‌ی ۴ را نشان می‌دهد.

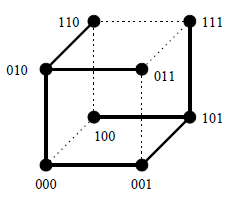نشان دهید که می‌توان یک درخت پر گل $T$ با $2^n$ رأس را در یک فوق مکعب $2^n$ رأسی $Q$ نشاند. یعنی می‌توان هر رأس $T$ را در یک رأس $Q$ قرار داد به طوری که دو راس مجاور در $T$ در $Q$ نیز مجاور هم باشند. به شکل مقابل برای $n=3 $ دقت کنید. روشن است که مسئله جواب‌های مختلف دارد و یکی کافی است.

الف) فقط با رسم شکل نشان دهید که چه گونه درخت پر گل ۱۶ رأسی را می‌توان در فوق مکعبی با ۱۶ رأس نشاند.

ب) این مسئله را برای حالت کلی حل کنید.