سیارهی آلفا
در سیارهی آلفا که اخیراً کشف شده، $ m×n$ کشور وجود دارد. اطلاعات زیر دربارهی این کشورها کشف شده است:
- $n≥3$ و $m≥3$.
- هر کشور با یک زوجِ مرتب از اعداد طبیعی بهصورت $(i,j)$ که $1≤j≤n$ و $1≤i≤m$ نامگذاری شده است.
- دو کشور $(i_1,j_1)$ و $(i_2,j_2)$ به هم جاده دارند، اگر و تنها اگر:
- $i_1=i_2$ و$|j_1-j_2|=1$.
- و یااینکه $i_1=i_2$ و $|j_1-j_2|=n-1$.
- و یا اینکه $j_1=j_2$ و $|i1-i2|=1$.
- و یا اینکه $j_1=j_2$ و $|i_1-i_2|=m-1$.
(در واقع هر کشوری به چهار کشورِ دیگر جاده دارد.)
دو جهانگرد قصد دارند با شروع از یک کشورِ دلخواه، هر کدام سفری را به تمامِ کشورها انجام دهند و از هر کشوری در طول سفر دقیقاً یکبار عبور کنند و سرانجام به کشور شروعِ سفر بازگردند. اما آن دو به دلایلی مایل نیستند از هیچ جادهای که قبلاً جهانگردِ دیگر از آن عبور کرده و یا در حال عبور است،عبور کنند.
ثابت کنید این دو نفر همواره میتوانند سفرهای خود را با موفقیت برنامهریزی کنند و به انجام برسانند.
در شکل زیر، ۳ مثال برای حالتهای $m=3$,$n=3$ و $m=3$,$n=4$ و $m=4$,$n=4$ کشیده شده است. خطوطِ نقطهچین مسیر سفر یکی و خطوطِ پررنگ مسیر سفر جهانگردِ دیگر است. در هر شکل، شهر $(i,j)$ در سطر $i$ و ستون $j$ قرار دارد.
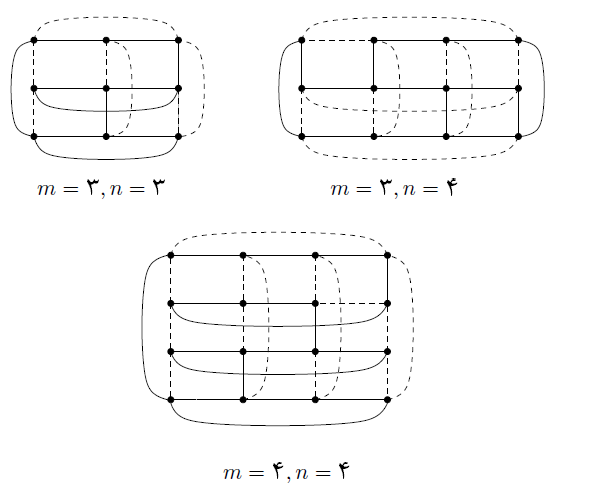
پاسخ
در اول نقشه کشور ها را با یک گراف شبکه (گرافی که رأس های آن نقاط شبکهاند) $ m×n$ مدلسازی میکنیم. یعنی هر کشور یک نقطه و هر جاده هم یک یال بین دو نقطه متناظر است. سفر مورد نظر جهانگردان نیز یک دور همیلتونی (دوری شامل تمامی نقاط شبکه) است. طبق گفته صورت سوال ما به دنبال پیدا کردن $2$ دور همیلتونی با یالهای مجزا هستیم.
تعریف:
یک یال را یال خوب سطر $i$ مینامیم اگر و تنها اگر این یال بین دو نقطه $(i,j_1)$ و $(i,j_2)$ کشیده شده و نیز $|j_1-j_2|=n-1$ باشد.
یک یال را یال خوب ستون $j$ مینامیم اگر و تنها اگر این یال بین دو نقطه $(i_1,j)$ و $(i_2,j)$ کشیده شده و نیز $|i_1-i_2|=m-1$ باشد.
نکته: فعلا حالت $n$ فرد و $m$ زوج از مسئله را حل نمیکنیم.
حال روی $n$ با گام $2$ تایی استقرا میزنیم. $ \Leftarrow $ زوجیت $n$ در حین استقرا ثابت میماند و نیز $m$ هم همیشه در حین استقرا ثابت است.
- فرض استقرا: $2$ دور همیلتونی یال مجزا در گراف شبکه $ m×n$ وجود دارد کهیکی از دور ها شامل دقیقا یک یال خوب سطری باشد و نیز این یال، یال خوب سطر آخر باشد.
- پایه استقرا:
- برای $n$های زوج: حالت $n=4$:
- برای $n$های فرد و $m$های فرد: حالت $n=3$ و $m$ فرد:
- گام استقرا: فرض میکنیم فرض استقرا برای گراف شبکه $m_0 \times n_0$ درست است این گراف را گراف شبکه اولیه مینامیم. طبق فرض استقرا در این گراف میتوان دو دور همیلتونی مجزا یافت کهیکی دقیقا یک یال خوب دارد و این یال، یال خوب سطر آخر است. این دور همیلتونی را دور خوب و دور همیلتونی مجزا از دور خوب را دور ناخوب مینامیم. حال میخواهیم فرض استقرا را برای گراف شبکه $m_0 \times ({n_0 +2 })$ اثبات کنیم. پس باید دو دور همیلتونی مجزا درون گراف شبکه $m_0 \times ({n_0 +2 })$ بیابیم کهیکی از دور ها دارای دقیقا یک یال خوب سطری آنهم در سطر آخر باشد. برای اینکار در قدم اول، دورهایمان را از روی دور همیلتونیهای شبکه $m_0 \times n_0$ میسازیم. بدین صورت کهیالهای شبکه $m_0 \times n_0$ وسطی (شامل ستون اول و آخر نباشد) از گراف شبکه $m_0 \times ({n_0 +2 })$ را مطابق با یکی از دورهای خوب یا ناخوب قرار میدهیم. دقت کنید یالهای خوب سطری میتوانند در دور همیلتونیهای فرض استقرا وجود داشته باشند ولی در شبکه $m_0 \times n_0$ وسطی به خاطر وجود ستونهای در سمت چپ و راست شبکه این یال نمیتوانند موجود باشند ولی موقتا ما این یالهای خوب سطری را به شبکه $m_0 \times n_0$ وسطی اضافه میکنیم.
- ساخت اولین دور همیلتونی: برای اینکار یالهای $m_0 \times n_0$ وسطی را منطبق با دور خوب در نظر میگیریم. در ادامهیالهای $(m_0,2) \leftrightarrow (m_0,1)$ و $(m_0,n_0+1)\leftrightarrow (m_0,n_0+2)$ را برای دور انتخاب میکنیم. سپس یالهای غیر خوب ستون اول و آخر و نیز یال $(1,1)\leftrightarrow (1,n_0+2)$ را هم انتخاب میکنیم. گفتیم کهیالهای خوب سطری موجود در فرض استقرا را باید از $m_0 \times n_0$ وسطی حذف کنیم. با توجه به اینکه دور خوب فقط یک یال خوب سطری داشت (آنهم در سطر آخر)، پس با حذف این یال کار را تمام کرده و دور به طور کامل انتخاب میشود. حال با توجه به اینکهیالهای $m_0 \times n_0$ وسط یک دور همیلتونی تشکیل میدادند، دور جدید نیز همه نقاط $m_0 \times n_0$ وسط را دیده و نیز تمامی نقاط دو ستون اول و آخر را هم میبیند پس این دور، دور همیلتونی است.
- ساخت دومین دور همیلتونی: در اول یالهای گراف شبکه $m_0 \times n_0$ وسط را منطبق با دور ناخوب اتخاب میکنیم. دقت کنید که درجه هر راس در هر دور همیلتونی $2$ است پس باید تمامی $4$ یال متصل به هر راس در اجتماع $2$ دور همیلتونیهای مجزا وجود داشته باشد، پس با توجه به اینکه دور خوب دقیقا یک یال خوب دارد و در دور همیلتونی دیگر این گراف شبکه (دور ناخوب) باید تمامی یالهای خوب ناموجود در دور خوب، وجود داشته باشد پس $m_0-1$ یال خوب سطری به ترتیب در سطرهای $1,2,3…,m_0-1$، در دور ناخوب وجود دارد. گقته بودیم کهیالهای خوب سطری دورهای همیلتونی فرض استقرا باید از شبکه $m_0 \times n_0$ وسطی دورمان حذف شوند. پس بجای یال خوب سطر $i$ ام در شبکه $m_0 \times n_0$ وسط ، $3$ یال $\lbrace (i,1) \leftrightarrow (i,2) , (i,1)\leftrightarrow(i,n_0+2) , (i,n_0+1)\leftrightarrow(i,n_0+2) \rbrace $ را برای دورمان اتخاب میکنیم. بجز برای $i=1$ و $i=m_0$ کهیالهای مورد نیاز در این دو حالت را جداگانه اضافه میکنیم. در حالت $i=1$ به خاطر اینکهیال خوب این سطر در اولین دور همیلتونی که ساختیم استفاده شده، پس فقط دو یال $\lbrace (i,1) \leftrightarrow (i,2) , (i,n_0+1)\leftrightarrow(i,n_0+2) \rbrace $ را انتخاب کرده و به جای یال خوب سطر $1$ یالهای خوب ستونهای $1$ و $n_0+2$ را انتخاب میکنیم. برای $i=m_0$ هم دو یال $\lbrace (m_0,1) \leftrightarrow (m_0,2) , (m_0,n_0+1)\leftrightarrow(m_0,n_0+2) \rbrace $ در ساخت دور همیلتونی$2$ استفاده شدهاند، پس در این حالت با توجه به اینکهیالهای خوب ستونهای اول و آخر در حالت قبل برای دور اتخاب شدهاند، ما فقط یال خوب سطر $m_0$ را اضافه میکنیم و بدین ترتیب ساخت دورمان تمام میشود و با توجه به نحوه چینش یالها و فرض استقرا مجموعهیالهای این دور یک دور همیلتونی را تشکیل میدهند.
- مجزا بودن: با کمی دقت متوجه میشوید کهیالهای دور همیلتونی$2$ مجزا از یالهای دور همیلتونی $1$ اند. زیرا طبق فرض استقرا و با توجه به نحوه ساخت دورها، تمامی یالهای انتخاب شده در گراف شبکه $m_0 \times n_0$ وسط در این دو دور همیلتونی از هم مجزااند و نیز یال هایی که ما در گام استقرا اضافه کردیم هم از هم مجزااند.
- کامل شدن فرض استقرا: حال در ساخت دور همیلتونی$1$ از یک یال خوب سطری استفاده شد که این یال، یال خوب سطر اول است. پس برای برآورده شدن کامل فرض استقرا باید دو گراف شبکه و دور همیلتونیها را نسبت به خط افق تقارن دهیم تا یال خوب سطری، سطر اول تبدیل بهیال خوب سطری، سطر آخر شده و نیز دو دور همیلتونی مجزا بمانند.
در طی گام استقرا زوجیت $m$ و $n$ حفظ میشود پس هیچ وقت از فرض استقرا برای گراف شبکه $m_0 \times n_0$ ای که $n$ فرد و $m$ زوج باشد، استفاده نشده و استقرا درست است.
حال برای بدست آوردن دورهای همیلتونی برای گراف شبکه $m \times n$ای که $n$ فرد و $m$ زوج باشد، جواب برای گراف شبکه $n \times m$ را درنظر بگیرید (چون تعداد ستون ها زوج است، وجود دارد). نقطه $(i,j)$ را به نقطه $(j,i)$ تناظر داده و نیز یالهای بین نقاط در حالت اولیه را تبدیل بهیالهایی بین نقاط متناظر کنید. بدین ترتیب دور ها مجزا و همیلتونی میمانند پس جواب برای این حالت نیز بدست میآید.
| ▸ سوال قبل | سوال بعد ◂ |