سوال ۱۷
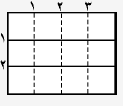
 یک تکه کاغذ به شکل مقابل در اختیار داریم:
یک تکه کاغذ به شکل مقابل در اختیار داریم:
دو نفر با نامهای $A$ و $B$ به این صورت بازی میکنند: $A$ در نوبت خودش یک تکه کاغذ را انتخاب کرده، با یک برش مستقیم روی یکی از خطوطی که با نقطه چین مشخص شدهاند، آن را به دو تکه تقسیم میکند. سپس $B$ نیز در نوبت خود همین کار را با یکی از تکههای کاغذ و خطوطی که به صورت کامل (غیر نقطه چین) کشیده شدهاند انجام میدهد. هر یک از بازیکنان که در نوبت خود نتواند بازی کند، بازنده محسوب میشود.
کدام یک از گزارههای زیر درستتر است؟
- اگر $A$ بازی را شروع کند، میتواند برنده شود.
- اگر $B$ بازی را شروع کند، میتواند برنده شود.
- در هر صورت $A$ میتواند برنده شود.
- در هر صورت $B$ میتواند برنده شود.
- هر بازیکنی که بازی را شروع کند میتواند برنده شود.
پاسخ
گزینه (۳) درست است.
در هر صورت $A$ میتواند برنده شود. خطوط تکه کاغذ را به شکل زیر شمارهگذاری میکنیم. اگر $B$ شروعکننده باشد به ناچار از یکی از سطرها ۱ یا ۲ کاغذ را به دو تکه تقسیم میکند. فرض میکنیم این شخص سطر ۱ را برش داده و تکه کاغذ را به دو تکه $a$ (قسمت بالایی) و$b$ (قسمت پایینی) تقسیم کند. در این صورت شخص$A$ از یکی از ستونهای ۱ و یا ۳ تکه $a$٬ آن را به دو تکه تقسیم میکند. $B$ ناچارا سطر ۲ از تکهی $b$ را برش میدهد و بازنده میشود زیرا چیزی برای برش دادن برای مرحلهی بعد برای او باقی نمیماند.
اگر $A$ شروعکننده باشد ابتدا او تکه کاغذ را از ستون ۲ برش میدهد. $B$ یکی از دو تکه را از سطر ۱ یا ۲ به دو تکه تقسیم میکند. شخص $A$ تکهی کوچکتر را انتخاب کرده و آن را به دو قسمت تقسیم میکند. شخص $B$ در نوبت خود سه بار دیگر میتواند تکه کاغذها را برش دهد و چیزی برای برش برای او باقی نخواهد ماند در صورتی که در هر مرحله برای شخص $A$ تکه کاغذ برای برش افزایش پیدا میکند.
| ▸ سوال قبل | سوال بعد ◂ |