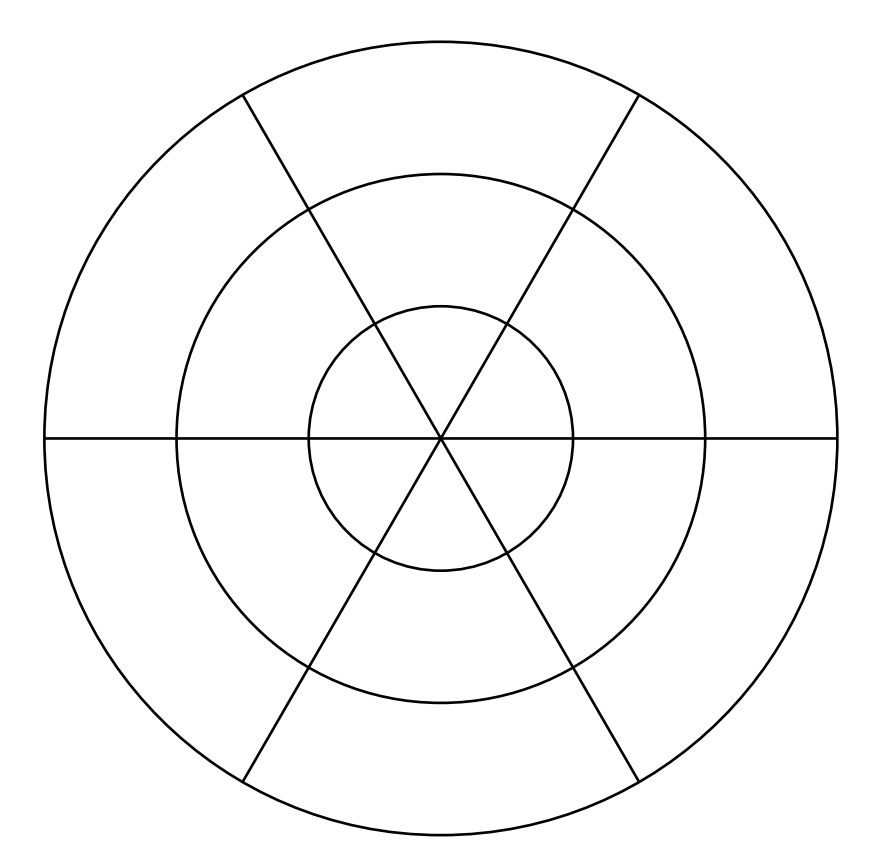
شکل زیر از سه لایه و شش قطاع تشکیل شده‌است که ١٨ خانه‌ی متفاوت ساخته‌اند. می‌خواهیم خانه‌ها را با اعداد ١ تا ١٨ شماره‌گذاری کنیم، طوری که شرایط زیر برقرار باشد:

• هیچ لایه‌ای نداشته باشیم که ضرب اعداد خانه‌های آن بر ٢۶ یا ٣٩ بخش‌پذیر باشد.
• ضرب اعداد هر قطاع بر ۶ بخش‌پذیر باشد.

به چند طریق این کار ممکن است؟

1. ۰
2. $(6!)^3 \times 2^6 \times (3!)^6$
3. $3 \times (6!)^3$
4. $(6!)^3 \times 2^6$
5. $(6!)^3 \times 2^6 \times 3$