گراف $G$ را به این شکل می‌سازیم: ابتدا به ازای هر یک از اعداد ۰ تا ۶۳ یک راس در نظر می‌گیریم. سپس بین هر دو راس که نمایش دودویی آن‌ها دقیقا در یک بیت اختلاف دارد یک یال رسم می‌کنیم.

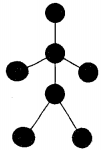
به هر زیرمجموعه‌ی ۷ تایی از راس‌های $G$ دقیقا شکل روبه‌رو را بسازند یک «آدمک» می‌گوییم. دقت کنید که بین راس‌های یک آدمک نباید هیچ یالی غیر از یال‌های نشان داده شده در شکل مقابل در گراف $G$ وجود داشته باشد.

در گراف $G$ چند آدمک می‌توان پیدا کرد؟

1. ۹۶۰۰
2. ۳۸۴۰
3. ۵۷۶۰
4. ۴۶۰۸۰
5. ۶۰۰

عدد یک آدمک را برابر با $XOR$ مقدار راس‌های آن در نظر می‌گیریم. مجموع اعداد تمام آدمک‌ها در گراف $G$ چند است؟

1. ۱۹۳۵۳۶۰
2. ۱۸۱۴۴۰
3. ۱۴۵۱۵۲۰
4. ۲۰۱۶
5. ۱۲۰۹۶۰