سوال ۳۷
مهرهی «رخ» در شطرنج٬ مهرهای است که تمامی خانههایی که همسطر٬ یا همستون با خودش باشند را تهدید میکند.
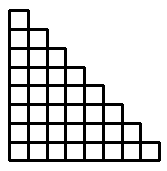
جدول پلکانی روبهرو را درنظر بگیرید. به چند طریق میتوان ۷ مهرهی «رخ» را در این جدول گذاشت٬ به طوری که هیچ دو مهرهای همدیگر را تهدید نکنند؟
- ۹۸۴
- ۲۵۵
- ۶۴۰
- ۲۸۲
- ۳۵
پاسخ
گزینهی (2) درست است.
ادعا میکنیم$k-1$ مهرهی رخ را میتوان به$2^k-1$ روش در پلکانی با $k$ ردیف پله چید. این ادعا را با استقرا ثابت میکنیم.
- پایهی استقرا: برای $k=1$ حکم برقرار است.
- گام استقرا: فرض کنیم برای $k-1$ ردیف پله، $2^{k-1}-1$ روش برای چیدن $k-2$ رخ وجود داشته باشد.
برای $k$ ردیف، بالاترین پله را در نظر میگیریم، دو حالت پیشمیآید:
- در این خانه رخ قرار دهیم. در اینصورت ستون سمت چپ حذف میشود و طبق فرض استقرا $k-2$ رخ باقیمانده به $2^{k-1}-1$ حالت چیده میشوند.
- در این خانه رخ قرار ندهیم. در اینصورت در هرکدام از $k-1$ ردیف باقیمانده بایدیک رخ وجود داشته باشد. چیدن آنهارا از ردیف بالا شروع میکنیم.گذاشتن یک رخ در این ردیف ۲ حالت دارد.برای هرکدام از ردیفهای دیگر هم با قراردادن رخهای قبلی، ۲ حالت بیشتر باقی نمیماند. پس طبق اصل ضرب $2^{k-1}$ حالت برای چیدن رخها وجود دارد.
بنابراین در مجموع $2^k-1$ راه برای چیدن رخها داریم و حکم ثابت شد. پاسخ مسئله به ازای $k=8$، ۲۵۵ میشود.
| ▸ سوال قبل | سوال بعد ◂ |