سوال ۳۸
یک کشور با ۹ شهر داریم. همانطور که در شکل میبینید، تعدادی جادهی یکطرفه بعضی از شهرها را به هم وصل کرده است. یک شهر، مثلِ $a$، را «خطرناک» میگوییم هرگاه شهر دیگری مثلِ $b$ وجود داشته باشد، به صورتی که بتوان از $a$ به $b$ رفت، اما نتوان از $b$ به $a$ بازگشت. دولت قصد دارد ۲ جادهی یکطرفهی جدید احداث کند، بهنحوی که در نهایت دقیقاً ۳ شهرِ غیر خطرناک در آن کشور باقی بماند.
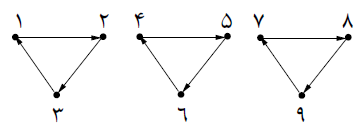
دولت به چند طریقِ مختلف میتواند این جادهها را احداث کند؟
- ۹
- ۸۱
- ۲۷
- ۴۸۶
- ۷۲۹
پاسخ
گزینه (۵) درست است.
شکل داده شده از سه مولفه $a$،$b$ و $c$ تشکیل شده است. برای ساختن شبکه مطلوب باید بهیکی از دو شکل $a \rightarrow b \rightarrow c$ و یا $a \rightarrow b \leftarrow c$ برسیم که تعداد کل حالات رسیدن به هر یک از آنها به ترتیب به شکل زیر بهدست میآید:
1)$a \rightarrow b \rightarrow c$
- انتخاب یک مولفه از سه مولفه برای آنکه نقش $a$ را بازی کند(این کار به ۳ طریق ممکن است).
- انتخاب یک راس از رئوس آن برای آنکه از آن راس فلشی خارج شود(این کار نیز به ۳ طریق ممکن است).
- انتخاب یک مولفه از دو مولفه باقیمانده برای آنکه نقش $b$ را بازی کند(این کار به ۲ طریق ممکن است).
- انتخاب یک راس از رئوس $b$ برای آنکه فلشی به آن وارد شود(به ۳ طریق).
- انتخاب یک راس از رئوس $b$ برای آنکه فلشی از آن خارج شود(به ۳ طریق).
- انتخاب یک راس از رئوس $c$ برای آنکه فلش خارج شده از $b$ به آن وارد شود(به ۳ طریق).
طبق اصل ضرب تعداد کل طرق در این حالت برابر $3\times3\times2\times3\times3\times3$ یعنی ۴۸۶ میشود.
2)$a \rightarrow b \leftarrow c$
- انتخاب یک مولفه از مولفه برای آنکه نقش $b$ را بازی کند(به ۳ طریق).[البته مشخص است که دو مولفه $a$ و $c$ همنقشند.]
- انتخاب یک راس از رئوس $a$ و یک راس از رئوس $c$ برای آنکه فلشهایی از آنها خارج شود($3\times3$ طریق).
- انتخاب یک راس از رئوس $b$ برای وارد شدن فلش خارج شده از $a$ و یک راس(نه لزوما متمایز از قبلی) از رئوس $b$ برای وارد شدن فلش خارج شده از $c$($3\times3$ طریق).
در این حالت نیز مجموع کل طرق برابر $3\times3^2\times3^2$ یعنی ۲۴۳ میشود.
باتوجه به حالتبندی فوق جواب مورد نظر $486+243$ یعنی ۷۲۹ بهدست میآید.
| ▸ سوال قبل | سوال بعد ◂ |