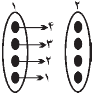
می‌خواهیم هر نقطه موجود در دسته‌ی $i+۱$ وصل کنیم ($i ≤۳$) به‌طوری‌ که هیچ دو نقطه‌ای از دسته‌ی $i$ام به‌یک نقطه از دسته‌ی $i+۱$ام وصل نباشند. هم‌چنین می‌خواهیم هر نقطه موجود در دسته‌ی ۴ را با یک پاره‌خط به دقیقاً یک نقطه در دسته‌ی ۱ وصل کنیم به‌طوری‌که هیچ دو نقطه‌ای از دسته ۴ به‌یک نقطه از دسته‌ی اول وصل نباشند. به چند طریق می‌توان این کار را انجام داد؟

1. $4^3×2^4×3^4$
2. $4^4×2^4×3^4$
3. $4^3×2^3×3^5$
4. $4^3×2^5×3^3$
5. $4^4×2^3×3^3$