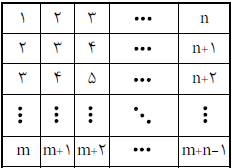
- تعریف زیر را برای سه سؤال بعدی درنظر بگیرید:
یک جدول $m\times n$ که در هر خانه آن یک عدد صحیح قرار میگیرد را شمارنده میگوییم. اگر اختلاف عدد نوشته شده در هر دو خانه مجاور (سطری یا ستونی) آن دقیقاً یک باشد. بهعنوان نمونه جدول روبهرو یک جدول شمارنده $2\times 3$ است.
سوال ۷
میخواهیم در حداقل تعداد خانههای یک جدول $m\times n$ عدد بگذاریم بهطوریکه در بقیهی خانهها فقط بهیک طریق بتوان عدد گذاشت تا حاصل یک جدول شمارنده باشد. این حداقل در چه بازهای قرار دارد؟
- ۱ یا ۲
- $[m+n-1,3]$
- $[{mn\over 2},m+n]$
- $[mn-1,{mn\over 2}]$
- دقیقاً $mn$
پاسخ
گزینه (۲) درست است.
اگر در خانهی بالا و سمت چپ جدول عدد ۱ و در خانهی پایین سمت راست جدول عدد $m+n-1$ را قرار دهیم آنگاه جدول به صورت منحصربهفرد٬ به شکل زیر پر خواهد شد:
سوال ۸
یک جدول شمارنده $m\times n$ که روی همهی خانههای آن را پوشانیدهاند، داده شده است. میخواهیم پوشش روی حداقل تعداد خانههای آن را برداریم (عددهای آن برای ما مشخص شود) که بتوانیم عدد بقیهی خانهها را حدس بزنیم. حداقل در چه بازهای قرار دارد؟
- ۱ یا ۲
- $[m+n-1,3]$
- $[{mn\over 2},m+n]$
- $[mn-1,{mn\over 2}]$
- دقیقاً $mn$
پاسخ
گزینه (۵) درست است.
در بعضی حالات خاص میتوان با دانستن اعداد بعضی از خانهها٬ عدد موجود در خانهای را کشف کرد ولی در حالت کلی جواب مورد نظر برابر $mn$ میباشد. برای رد گزینه ۴ گزینهی دیگر میتوانید جدول $2\times 2$ را برسی کنید.
سوال ۹
چند جدول شمارندهی $2\times 5$ وجود دارد که در خانه بالا و سمت چپ آن عدد یک قرار داده شده است؟
- بین ۱ تا ۴۰ عدد
- بین ۴۱ تا ۱۳۰ عدد
- بین ۱۳۱ تا ۲۰۰ عدد
- بین ۲۰۱ تا ۲۸۰ عدد
- بیش از ۲۸۰ عدد
پاسخ
گزینه (۳) درست است.
خانه $(2,1)$ به دو طریق قابل پر شدن میباشد(۰ و یا ۲) و هر یک از ستونهای چهارگانه دیگر متناسب با ستون قبلی خود به سه طریق میتوانند پر شوند٬ بنابراین طبق اصل ضرب جواب مورد نظر $2\times3^4$ یعنی ۱۶۲ میباشد.
| ▸ سوال قبل | سوال بعد ◂ |