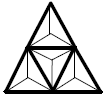
سوال ۲۵
 به چند طریق میتوان مثلثهای کوچک را سیاهیا سفید کنیم٬ بهطوریکه هیچ دو مثلث سیاه مجاور نباشند. (دو مثلث مجاورند اگر ضلع مشترک داشته باشند.)
به چند طریق میتوان مثلثهای کوچک را سیاهیا سفید کنیم٬ بهطوریکه هیچ دو مثلث سیاه مجاور نباشند. (دو مثلث مجاورند اگر ضلع مشترک داشته باشند.)
- ۱۰۸
- ۱۱۲
- ۱۴۴
- ۱۹۴
- ۲۰۸
پاسخ
گزینه (۵) درست است.
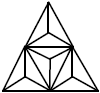
با در نظر گرفتن ۴ مثلث پر رنگ در شکل زیر حالات زیر پیش میآید:
- تعداد مثلثهای سیاه صفر باشد که این کار به $\binom{12}{0}$؛ یعنی ۱ طریق ممکن است.
- تعداد مثلثهای سیاهیک باشد که این کار به $\binom{12}{1}$؛ یعنی ۱۲ طریق ممکن است.
- تعداد مثلثهای سیاه دو باشد که در این صورت آن دو مثلث نمیتوانند در داخل یک مثلث پر رنگ قرار گیرند. رنگ کردن دو مثلث با شرط فوق به $\binom{4}{2} \times \binom{3}{1} \times \binom{3}{1}-3$؛ یعنی ۵۱ طریق ممکن است.
- تعداد مثلثهای سیاه ۳ باشد که در این صورت آن سه مثلث در داخل سه مثلث پررنگ متمایز قرار داشته و به $\binom{4}{2} \times \binom{3}{1} \times \binom{3}{1} \times \binom{3}{1} - \binom{3}{1} \binom{6}{1}$؛ یعنی ۹۰ طریق امکانپذیر است.
- تعداد مثلثهای سیاه ۴ باشد که در این صورت آن چهار مثلث در داخل چهار مثلث پررنگ متمایز قرار داشته و به $\binom{3}{1} \binom{2}{1} \binom{3}{1} \binom{3}{1}$؛ یعنی ۵۴ طریق ممکن است.
مجموع کل حالات بهدست آمده $1+12+51+90+54$؛ یعنی ۲۰۸ میشود.
| ▸ سوال قبل | سوال بعد ◂ |