سوال ۱۹
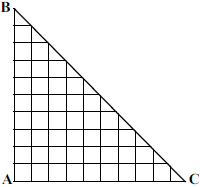 فردی از محل $A$ میخواهد با حرکتهای افقی و عمودی به نقطهای از خیابان اصلی شهر برسد (ضلع ($BC$ برسد بهطوری که مسیری که طی میکند کوتاهترین مسیر باشد و از ابتدای شروع حرکت تا انتها دقیقاً در ۳ مکان تغییر جهت بدهد. (ضلعهای $AB$ و $AC$ به ۱۰ قسمت مساوی تقسیم شدهاند(. وی به چند طریق میتواند مسیر خود را انتخاب کند؟
فردی از محل $A$ میخواهد با حرکتهای افقی و عمودی به نقطهای از خیابان اصلی شهر برسد (ضلع ($BC$ برسد بهطوری که مسیری که طی میکند کوتاهترین مسیر باشد و از ابتدای شروع حرکت تا انتها دقیقاً در ۳ مکان تغییر جهت بدهد. (ضلعهای $AB$ و $AC$ به ۱۰ قسمت مساوی تقسیم شدهاند(. وی به چند طریق میتواند مسیر خود را انتخاب کند؟
- ۱۶۸
- ۲۴۰
- ۱۲۰
- ۸۴
- ۱۰۲۴
پاسخ
گزینه (۱) درست است.
فرض میکنیم حرکت اول به سمت راست باشد در این صورت برای رسیدن به $BC$ ده واحد طی خواهد شد که آن را به صورت $aaaaaaaaaa$ نمایش میدهیم. هدف قرار دادن سه علامت به نشانهی مکانهای تغییر جهت در بین $a$ها میباشد که این امر به $\binom{9}{3}$ یعنی ۸۴ طریق امکانپذیر است( بین هر دو $a$ متوالی یک جا خالی برای قرار دادن مکاننما وجود دارد و بین ده عدد $a$ مجموعا نه جا خالی وجود دارد).
اگر حرکت اول به سمت بالا باشد نیز برای رسیدن به $BC$ به ۸۴ طریق میتوان عمل کرد که مجموع کل مسیرهای مطلوب $84+84$ یعنی ۱۶۸ خواهد شد.
| ▸ سوال قبل | سوال بعد ◂ |