سوالات المپیاد:مرحله ی اول:دوره ی ۱۱:سوال ۸
سوال ۸
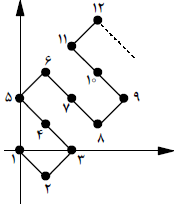 اعداد۳٬۲٬۱ و … را مطابق شکل بر روی صفحهی مختصات مینویسیم.
این اعداد بهترتیب در مختصات (0,0) (1, -1) ،(2, 0)٬ و … قرار دارند.
مختصات نقطهی متناظر عدد ۱۳۷۹ چیست؟
اعداد۳٬۲٬۱ و … را مطابق شکل بر روی صفحهی مختصات مینویسیم.
این اعداد بهترتیب در مختصات (0,0) (1, -1) ،(2, 0)٬ و … قرار دارند.
مختصات نقطهی متناظر عدد ۱۳۷۹ چیست؟
- (458, 460)
- (229, 231)
- (459, 461)
- (916, 918)
- (917, 919)
پاسخ
اگر یک دورهی تناوب از شکل را در نظر بگیریم و مختصات نقطهی A به صورت (k,k) باشد٬ آنگاه اولا K فرد است. ثانیا در نقاط E،D،C،B،A و F به ترتیب اعداد 3k+5،3k+4،3k+3،3k+2،3k+1 و 3k+6 قرار دارد. عدد ۱۳۷۹ به صورت 3k+2 میباشد. بنابراین آن عدد در نقطهی B قرار دارد. چون از تساوی 3k+2=1379 مقدار K برابر ۴۵۹ بهدست میآید. پس مختصات نقطهی A به صورت (459,459) و مختصات نقطهی B به صورت (458,460) خواهد بود.