فهرست مندرجات
زوجیت
در این صفحه با زوجیت آشنا می‌شوید.
تعریف
زوجیت روی یک عدد تعریف می‌شود. منظور از زوجیت، زوج بودن یا فرد بودن یک عدد است. هرگاه می‌گوییم زوجیت یک چیز ثابت می‌ماند، به معنای آن است که آن عدد اگر فرد است، فرد می‌ماند و اگر زوج است، زوج می‌ماند. در بسیاری از مسائل کافی است یک چیز تعریف کنیم و با توجه به تغییرات زوجیت آن مسئله را حل کنیم.
مثال: یک جدول $8 \times 8$ داریم که در ابتدا یک گوشه‌ی آن سیاه است و بقیه‌ی خانههای آن سفید هستند. در هر مرحله می‌توان یک سطر یا یک ستون در نظر گرفت و رنگ تمام خانههای آن را عوض کرد (از سیاه به سفید و بالعکس). آیا می‌توان کاری کرد که تمام خانههای جدول سیاه شوند؟
پاسخ
خیر؛ تعداد خانههای سیاه جدول را در نظر بگیرید. یک گام را در نظر بگیرید و بدون از دست دادن کلیت فرض کنید در آن سطر یا ستونی با $b$ خانه‌ی سیاه را تغییر وضعیت داده‌ایم. پس تعداد خانههای سیاه آن سطر یا ستون $8-b$ تا خواهد شد. بنابراین تغییرات تعداد خانههای سیاه کل جدول برابر با $(8-b)-b=8-2b$ است که عددی زوج است. پس زوجیت تعداد خانههای سیاه جدول در حین مراحل تغییری نمی‌کند. از آن‌جایی که در ابتدا ۱ و در انتها ۶۴ خانه‌ی سیاه داریم، این کار امکان‌پذیر نیست.
یک در میان‌ها
در برخی از مسائل یک روند به صورت یک در میان رخ می‌دهد. این مسائل نیز از نوع زوجیت هستند. به مثال زیر توجه کنید:
مثال:
آیا ممکن است خرخ‌دنده‌های سیستم زیر به طور هماهنگ و مناسب بچرخند؟
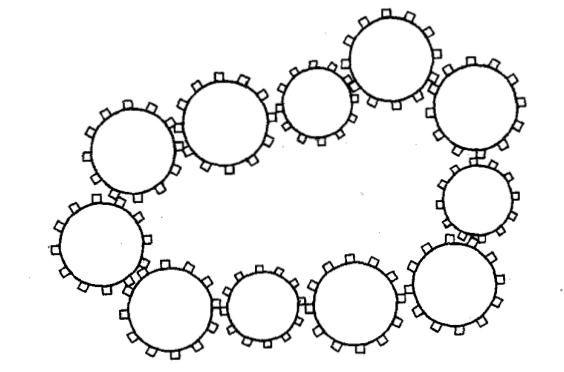
پاسخ
خیر؛ اگر یک خرچ‌دنده به صورت ساعت‌گرد بچرخد، چرخ‌دنده‌‌های مجاور آن باید به صورت پادساعت‌گرد بچرخند و بالعکس. پس چرخ‌دنده‌ها باید به صورت یک در میان ساعت‌گرد و پادساعت‌گرد بخرچخند. از آن‌جایی که تعداد چرخ‌دنده‌ها فرد است، این کار ممکن نیست.
چند مثال
مثال: آیا می‌توان به جای هر یک از علامت‌های $*$ در عبارت زیر یکی از علامت‌های $+$ یا $-$ را گذاشت؛ طوری که عبارت درستی به دست آید؟ $$*1*2*...*1000 = 1395$$
پاسخ
خیر؛ فرض کنید بتوان با شرایط گفته شده علامت‌گذاری کرد. در ابتدا تمام علامت‌ها را $+$ بگذارید تا عبارت سمت چپ برابر $\frac{1000 \times 1001}{2} = 500500$ شود که عددی زوج است. حال یکی‌یکی علامت‌هایی که باید $-$ شوند را منفی کند. هر گاه $+a$ به $-a$ تبدیل شود، از حاصل به مقدار $2a$ (مقداری زوج) کم می‌شود؛ پس حاصل زوج خواهد ماند و نمی‌تواند برابر ۱۳۹۵ شود.
مثال: ۳ توپ قرمز، آبی و سبز روی میز هستند و در ابتدا هم‌خط نیستند. در هر مرحله یک توپ را با ضربه‌ای از میان دو توپ دیگر رد می‌کنیم (مانند بازی سه‌توپ). آیا ممکن است پس از ۲۵ مرحله هر توپ به جای نخست‌ش بازگردد؟
پاسخ
خیر؛ با شروع از توپ قرمز، توپ‌ها را در جهت ساعت‌گرد بخوانید. بدون از دست دادن کلیت مسئله فرض کنید در ابتدا این ترتیب به صورت قرمز، آبی و سبز باشد. به این ترتیب در مراحل به طور یک در میان ترتیب‌های زیر را خواهیم دید:
- قرمز، سبز، آبی
- قرمز، آبی، سبز
بنابراین بعد از فرد مرحله امکان ندارد به وضعیت آغازین بازگردیم.
مسائل نمونه از المپیادهای کامپیوتر ایران
منابع و مراجع
- D.Fomin, I.Itenberg, S.Genkin (1996), Mathematical circles (Russian Experience), Mathematical World
- Arthur Engel (1998), Problem Solving Strategies, New York, Springer
خواننده‌ی گرامی، لطفا در صورت داشتن پیشنهاد یا مشاهده‌ی مشکل (علمی، تایپی و …) در این صفحه، به ما اطلاع دهید:
ابزار صفحه
کلیه‌ی حقوق این سایت متعلق به کمیته‌ی ملی المپیاد کامپیوتر ایران است.
نظرات