سوال ۲۲
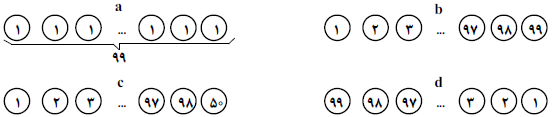
$99$ ظرف با تعدادی گردو در هریک موجود است، این ظرفهاروی یک میز به صورت یک صف قرار گرفتهاند. هرجا میتوانیم ۲ ظرف کنار هم را انتخاب میکنیم و از هر کدام ۱ گردو برداریم (هر دو باید حداقل ۱ گردو داشته باشند)،یا به هر کدام ۱ گردو اضافه میکنیم. دو وضعیت از ظرفها را قابل تبدیل به هم مینامیم اگر بتوان با شروع از هر کدام و با چند بار انجام این دو حرکت٬ به دیگری رسید. چند زوج متمایز از چهار وضعیت $a$، $b$، $c$ و $d$ به هم قابل تبدیلاند؟
- ۰
- ۱
- ۲
- ۳
- ۶
پاسخ
گزینه (؟) درست است.
در هر مرحله دو گردو به کل گردوها اضافه و یا دو گردو از کل گردوها کم میشود٬ بنابراین اگر کل گردوها فرد باشد در نهایت نیز فرد و اگر کل گردوها زوج باشد در نهایت نیز کل گردوها زوج خواهد بود.
مجموع کل گردوها در حالات $a$، $b$، $c$ و $d$ به ترتیب فرد٬ زوج٬ فرد و زوج میباشد٬ بنابراین $a$ به $a،b$ به $c،d$ به $b$ و $c$ به $d$ قابل تبدیل نیستند و اما $a$ به $c$ و نیز $b$ به $d$ قابل تبدیلاند که نحوهی تبدیل هر یک به شکل زیر میباشد:
نحوهی تبدیل $a$ به $c$:اولی را رد کرده و پس از آن هر زوج متوالی را انتخاب کرده و گردو به آنها اضافه میکنیم.
- اولی٬دومی و سومی را رد کرده و پس از آن هر زوج متوالی را انتخاب کرده و گردو به آنها اضافه میکنیم.
- اولی٬دومی و سومی٬ چهارمی و پنجمی را رد کرده و پس از آن هر زوج متوالی را انتخاب کرده و گردو به آنها اضافه میکنیم.
اگر الگوریتم فوق را ادامه دهیم به حالت $c$ خواهیم رسید.
نحوهی تبدیل $b$ به $d$:
- زوجهای $(98,99)،…،(52,53)،(50,51)،(49,50)،…،(3,4)،(1,2)$ را انتخاب کرده و به هر یک از اعضای ۲۵ زوج اول یک گردو اضافه واز هر یک از اعضای ۲۵ زوج دیگر یک گردو برمیداریم که به دنبالهی یر خواهیم رسید:
$$2,3,4,5,…,49,50,51,…,95,96,97,98$$
- زوجهای $(48,49)،…،(4,5)،(2,3)$ را انتخاب کرده و به هر یک از اعضای آن زوجها یک گردو اضافه و زوجهای $(99,98)،…،(53,54)،(51,52)$ را انتخاب کرده و از هر یک از اعضای آن یک گردو برمیداریم که به دنبالهی زیر خواهیم رسید:
$$3,4,5,…,49,50,50,50,50,50,51,…,95,96,97$$
با تکرار الگوریتم فوق پس از مدتی به دنبالهی متقارن زیر میرسیم:
$$50,51,50,…,50,51,50,51,50,50,50,51,50,51,50,…,50,51,50$$
باز باتکرار آن الگوریتم به دنبالهی $d$ خواهیم رسید.
| ▸ سوال قبل | سوال بعد ◂ |