گزینه (۴) درست است.

تعداد حالاتی که صفر خانه علامت زده شده باشد برابر $\binom{8}{0}$ یعنی ۱ می‌باشد.

تعداد حالاتی که‌یک خانه علامت‌ زده شده باشد برابر $\binom{8}{1}$ یعنی ۸ می‌باشد.

تعداد حالاتی که دو خانه علامت‌ زده شده باشد برابر $\binom{8}{2}$ یعنی ۲۸ می‌باشد که در ده مورد خانه‌ها مجاور هستند و ۱۸ مورد از آن مطلوب می‌باشد.

تعداد حالاتی که سه خانه‌ی علامت‌زده شده مطلوب باشند برابر ۱۲ می‌باشد که به شکل زیر می‌باشند:

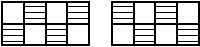
و بالاخره تعداد حالاتی که چهار خانه‌ی علامت‌ زده شده باشند برابر ۲ می‌باشد که به شکل زیر می‌باشند:

مجموع کل حالات اشاره شده ۴۱ می‌شود.