توابع بازگشتی
تعریف
به تابعی بازگشتی میگوییم که در روند اجرا خودش را فراخوانی کند . شاید به نظر برسد که در چنین حالتی برنامه هیچوقت به پابان نمیرسد ولی همیشه اینطور نیست اگر تابع ما شرایط خاصی داشته باشد و حالت پایه برای آن تعریف شده باشد روند اجرای آن به پایان میرسد و نتیجه مورد نظر بدست میآید.
- باید برای مسئله حداقل یک حالت پایه تعریف کرده و مقدار تابع را در آن حالت بدانیم.
- روند فراخوانی ها باید به حالت(های) پایه ختم شود و به دور منجر نشود.
مثال اول
میخواهیم تابعی بازگشتی برای محاسبه تابع $F(n)=n!$ بنویسیم.
- fac.cpp
int fac(int n){ if(n<=0) return 1; return n*fac(n-1); }
حال روند محاسبه $fac(3)$ را بررسی میکنیم . $fac(3)$ صدا میشود و سپس $fac(2)$ را صدا میکند و سپس $fac(1)$ صدا میشود و خروجی $1$ را برمیگرداند در تابع $fac(2)$ این مقدار در $2$ ضرب شده و مقدار $2$ به عنوان خروجی $fac(2)$ به تابع $fac(3)$ فرستاده میشود و این مقدار در $3$ ضرب میشود و مقدار $6$ به عنوان خروجی برگردانده میشود.
مثال دوم
میخواهیم تابعی بنویسیم که مقدار جمله $n$ ام فیبوناچی را محاسبه کند.
- fibo.cpp
int fibo(int n){ if(n<=1) return 1; return fibo(n-1)+fibo(n-2); }
روند محاسبه $fibo(5)$ به این شکل است :
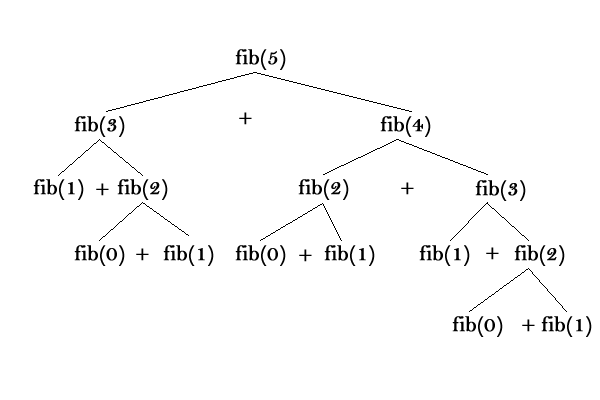
مثال سوم
تابعی بازگشتی بنویسید که مقدار $p$ $mod$ $n^k$ را در $O(lgk)$ محاسبه کند.
پاسخ
- modPow.cpp
int modPow(int n,int k,int p){ if(k==0) return n%p; int ret=modPow(n,k/2,p); ret=(temp*temp)%p; if(k%2==1) temp=(temp*n)%p; return temp; }