مرتب سازی حبابی
تعریف
مرتب سازی حبابی (Bubble Sort) نوعی مرتبسازی مقایسهای ساده است که در آن فهرست دادهها را تا جایی که مرتب شوند پیمایش میکند و عناصر مجاور را باهم مقایسه میکند و اگر در ترتیب نادرست بودند آنها را جابهجا میکند.
این مرتب سازی از این جهت حبابی نامیده میشود که عناصر بزرگتر در آن مانند حباب به آخر لیست میآیند. با وجود این که الگوریتم آن بسیار ساده است اما به علت کندی ناکارآمد میباشد و برای حل بیشتر مسائل مناسب نیست.
الگوریتم
شبه کد این الگوریتم به صورت زیر میباشد:

در شبه کد بالا هر بار که حلقه تمام میشود بزرگترین عنصر به آخر آرایه میرسد و در حلقههای بعدی وقتی به این خانه میرسیم جابهجایی صورت نمیگیرد.
این الگوریتم را میتوان با اندکی تغییر بهتر کرد چون که در مرحلهی $x$ام, $x$امین بزرگترین عنصر پیدا میشود پس نیاز نیست که در هر بار اجرای حلقه تا پایان لیست برویم. شبه کد زیر آن را دقیقتر توصیف میکند:
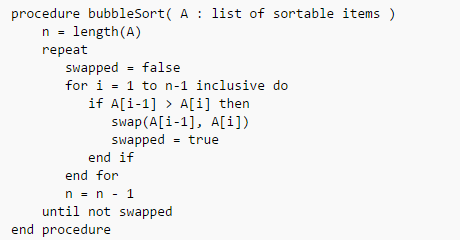
پیچیدگی الگوریتم
در بدترین حالت حلقه بیرونی باید $n-1$ بار اجرا شود و در مرحلهی $i$ام باید $n - i$ عمل انجام شود. پس در مجموع به $\frac{n(n-1)}{2}$ که از $\mathcal{\Theta}(n^2)$ عمل میباشد نیاز است. پس این الگوریتم از $\mathcal{O}(n^2)$ میباشد. در بهترین حالت تنها یکبار وارد حلقه میشود و از $\mathcal{O}(n)$ میباشد. در حالت میانگین نیز از $\mathcal{O}(n^2)$ میباشد. الگوریتمهای مرتبسازی بسیاری وجود دارند که بدترین زمان اجرای آنها از این بهتر است یا پیچیدگی متوسط آنها $\mathcal{O}(n \log n)$ است. حتی بقیه اگوریتمهای مرتبسازی از $\mathcal{O}(n^2)$ مثل مرتبسازی درجی، عملکرد بهتری نسبت به مرتبسازی حبابی از خود نشان میدهند.
پیادهسازی سریع تر
- bubble_Sort.cpp
#include <iostream> #include <algorithm> using namespace std; const int maxn=1000+100; int n,a[maxn]; int main() { cin>>n; for(int i=1;i<=n;i++) cin>>a[i]; for(int i=1;i<=n;i++){ bool swaped=0; for(int j=1;j<=n-i;j++) if(a[j]>a[j+1]){ swap(a[j],a[j+1]); swaped=true; } if(!swaped) break; } for(int i=1;i<=n;i++) cout<<a[i]<<endl; return 0; }