سوالات المپیاد:مرحله ی دوم:دوره ی ۷:سوال ۶
مرتب کردن دیسکها
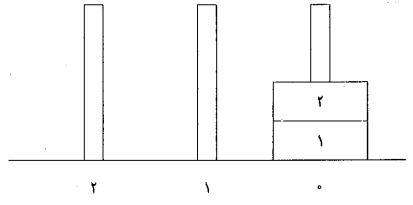
تعداد 2k دیسک داریم که روی هر کدام، یکی از عددهای ۱ تا 2k نوشته شده است. k+2 میله با شمارههای صفر تا k+1 در یک ردیف پست سر هم قرار گرفتهاند. در ابتدا، دیسکها با یک ترتیب داده شده در میلهی صفر روی هم قرار دارند. در هر حرکت میتوان بالاترین دیسک موجود روی میلهی i ام را برداشته و روی دیسکهای میلهی i+1 ام قرار داد (0≤i≤k). این حرکت را با Ti نمایش میدهیم. حالت نهایی مرتب، حالتی است که در آن تمام دیسکها به ترتیب از شمارهی ۱ تا 2k (پایین به بالا) روی میلهی شمارهی k+1 قرار گرفته باشند. برای مثال، به ازای k=1 دنبالهی حرکتهای لازم برای رسیدن به حالت نهایی مرتب از حالت اولیهای به شکل زیر میتواند به صورت (T0,T0,T1,T1) باشد.
ثابت کنید به ازای هر k میتوان از هر ترتیب اولیهی دیسکها روی میلهی شمارهی صفر به یک حالت نهایی مرتب رسید.