شکلات تخت
حامد و امیرمهدی یک شکلات تخت به صورت جدولی $n \times n$ در اختیار دارند. آنها می‌خواهند در حین خوردن شکلات یک بازی نیز باهم انجام دهند. بازی به این صورت است:
حامد از گوشه بالا چپ و امیرمهدی از گوشه پایین راست بازی را شروع می‌کند و به نوبت بازی می‌کنند. اولین حرکت را حامد انجام می‌دهد. هر کس در نوبت خودش باید تکه‌ای مستطیلی (که شامل گوشه خودش باشد) را گاز بزند و حتما باید یک خانه از شکلات را بخورد (در واقع نمی‌تواند مستطیلی را انتخاب کند که همه خانه‌هایش در نوبت‌های قبلی خورده شده باشند). کسی که آخرین تکه از شکلات را بخورد بازنده است. نشان دهید امیرمهدی همیشه می‌تواند طوری بازی کند که برنده شود.
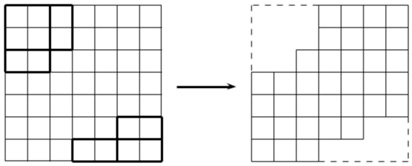
در شکل زیر حالتی نشان داده شده است که حامد و امیرمهدی هر کدام دو نوبت بازی می‌کنند و در نوبت‌هایشان مستطیل‌های پررنگ را می‌خورند. شکل سمت راست شکلات باقی‌مانده پس از این حرکات را نشان می‌دهد.
پاسخ
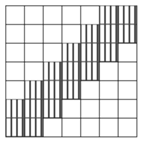
شکل زیر را در نظر بگیرید:
در واقع قطر فرعی به همراه دو قطر پایینی و بالایی آن هاشور خورده‌اند. می‌خواهیم نشان دهیم نفر دوم همیشه می‌تواند طوری عمل کند که شکل نسبت به قطر فرعی قرینه باشد و هیچ یک از مربع‌های قسمت هاشور خورده، خورده نشده باشند. توجه کنید که در صورتی که بازی به جدولی به اندازه ۱ یا ۲ با خاصیت فوق برسد به‌راحتی می‌توان نشان داد که نفر دوم می‌تواند برنده شود(چرا؟).
فرض کنید یک جدول قرینه نسبت به قطر فرعی که خانه‌های هاشور خورده آن سالم است به نفر اول می‌رسد(در اول کار این شرط برقرار است). در این صورت برای حرکت نفر اول دو حالت وجود دارد:
- هیچ یک از خانه‌های هاشور خورده، خورده نمی‌شوند.
- مستطیل خورده شده توسط نفر اول شامل حداقل یک خانه‌ی هاشور خورده می‌باشد.
در حالت اول نفر دوم می‌تواند قرینه حرکت نفر اول را نسبت به قطر فرعی انجام دهد(چرا؟).
در حالت دوم یا کل جدول خورده شده است یا نفر دوم می‌تواند یک جدول کوچک‌تر با شرایط گفته شده ایجاد کند(چرا؟).
همان‌طور که می‌دانیم در هر حرکت حداقل یک خانه خورده می‌شود در نتیجه تعداد خانه‌های باقی‌مانده در حال کم شدن است و حتما در جایی یا نفر اول کل شکلات را می‌خورد یا به یک شکلات $2\times2$ یا $1\times1$ می‌رسد.
ابزار صفحه
کلیه‌ی حقوق این سایت متعلق به کمیته‌ی ملی المپیاد کامپیوتر ایران است.
