رشته‌ی $S$ را با $n$ حرف در نظر بگیرید. مجموعه‌ی جایگشت‌های دوری $S$ به نام $R$ را به‌صورت $R$={$S_1,S_2,…,S_n$} نشان می‌دهیم به‌طوری‌ که $S_1=S$ و $S_{i+1}$ ($1 \le i \lt n$) را از $S_i$ به این شرح به دست می‌آوریم: حرف انتهایی $S_i$ را برمی‌داریم و در اول رشته‌ی باقیمانده قرار می‌دهیم.

یک روش رمز کردن رشته‌ی $S$ به این صورت است: رشته‌های $S_1$ تا $S_n$ را به ترتیب الفبایی مرتب می‌کنیم و رشته‌های مرتب‌شده را به ترتیب در سطرهای یک جدول $n×n$ قرار می‌دهیم. مثلاً جدول متناظر رشته‌ی banan مطابق شکل زیر است:

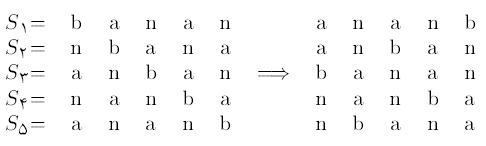
رمز شده‌ی رشته $S$ از دو قسمت تشکیل شده است: قسمت اول رشته‌ای است که از حروف ستون آخر جدول از بالا به پایین به دست می‌آید و قسمت دوم شماره‌ی سطر $S$ در جدول است. با توجه به جدول بالا رمز شده‌ی banan، زوج (bnnaa,۳) است. ثابت کنید این روش رمز کردن برگشت‌پذیر است. به‌عبارت‌ دیگر ثابت کنید می‌توان از هر زوج رمز شده‌ی متناظر یک‌رشته، به رشته‌ی منحصربه‌فرد اولیه رسید. روشی برای به دست آوردن رشته‌ی اولیه بیان کنید. روش خود را به‌ صورت دقیق و گام‌به‌گام بیان کنید و مراحل مختلف آن را برای رمز یابی زوج (sfaraf,۶) نشان دهید.

• سوال بعد
• سوال قبل