کمپانی پستی ‎$ ‎AHPC‎ $‎ برای رساندن نامه‌ها یک استراتژی ساده دارد. کمپانی به دنبال یک داوطلب می‌گردد‏، برای او ارزان‌ترین بلیط سفر هوایی از مبدا به مقصد را می‌خرد و بسته را در فرودگاه مبدا به داوطلب می‌دهد تا در فرودگاه مقصد تحویل دهد.

علاوه بر پرواز هوایی مستقیم بین مبدا و مقصد‏، پروازهای غیر‌مستقیم که در چندین فرودگاه میانی توقف می‌کنند نیز وجود دارد.در پرواز غیرمستقیم مسافران در فرودگاه مبدا سوار می‌شوند و به صورت متوالی در تمامی فرودگاه‌های میانی خواهند بود. البته در پرواز غیر‌مستقیم آنها می‌توانند در هر کدام از فرودگاه‌های میانی سفر خود را ادامه ندهند. در پروازهای غیر‌مستقیم هزینه ثابت است و ادامه ندادن بخشی از مسیر باعث بازگشت قسمتی از هزینه‌ی سفر نخواهد شد. یک سفر هوایی می‌تواند شامل پروازهای مستقیم و پروازهای غیر‌مستقیم و هر دو باشد.

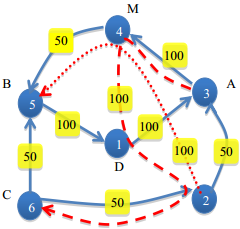
به خاطر مسائل اقتصادی کمپانی به دنبال روشی برای کاهش هزینه‌هایش می‌باشد. یک جفت بسته را در نظر بگیرید‏، یکی قرار است از ‎$ ‎A‎ $‎ به ‎$ ‎B‎ $‎ و دیگری از ‎$ ‎C‎ $‎ به ‎$ ‎D‎ $‎ برده شوند.(‎$ ‎A‎ $‎ و ‎$ ‎B‎ $‎ و ‎$ ‎C‎ $‎ و ‎$ ‎D‎ $‎ فرودگاه‌های متمایزی هستند.) کمپانی ممکن است دو بلیط سفر برای دو داوطلب یکی از ‎$ ‎A‎ $‎ به ‎$ ‎B‎ $‎ و دیگری از ‎$ ‎C‎ $‎‎ به ‎$ D $‎ بخرد. اگر این دو سفر در فرودگاه ‎$ ‎M‎ $‎ مشترک باشند(‎$ ‎‎M‎ $‎ لازم نیست با بقیه متمایز باشد.) دو داوطلب می‌تواننند در ‎$ ‎M‎ $‎ یکدیگر را ببینند و بسته‌هایشان‎ را عوض کنند. کمپانی نیز مطمئن است بسته‌ها به مقصد رسیده و هزینه‌ی کل ممکن است کاهش یافته باشد. برای مثال در شکل ‎$ ‎6‎ $‎ زیر فرودگاه وجود دارد که پروازهای مستقیم با خطوط تیره و پروازهای غیر‌مستقیم با خط‌چین و نقطه‌چین نشان داده شده‌اند.(هزینه‌ی مسیرها روی آنها درج شده است.) یک بسته باید از فرودگاه به ‎$ ‎3‎(‎A‎)‎‎ $‎ و ‎$ ‎5‎(B)‎‎ $‎ یکی از ‎$ ‎6(C)‎ $‎ به ‎$ ‎1(D)‎ $‎ برده شوند. کمپانی می‌تواند برای نفر اول بلیط ‎$ ‎(3,4),(4,5)‎‎‎ $‎ و برای نفر دوم بلیط ‎$ ‎(6,5),(5,1)‎ $‎ را بخرد که هزینه‌ی کل ‎$ ‎300‎ $‎ خواهد شد. یک راه حل هم می‌تواند به این صورت باشد که برای نفر اول بلیط ‎$ ‎(3,4,1,2,6)‎ $‎ و نفر دوم‎ ‎‎بلیط $ ‎(6,2),(2,4,5) ‎$‎ را بخرد‏، که هزینه ‎$ ‎250‎ $‎ را خواهد داشت. دو نفر در فرودگاه ‎$ ‎4‎ $‎ یک‌دیگر را می‌بینند و بسته‌هایشان را عوض می‌کنند‏، نفر اول نیز در فرودگاه ‎$ ‎1‎ $‎ مسیر را ادامه نمی‌د‎هد.

شما باید برنامه‌ای بنویسید که با داشتن اطلاعات پرواز کم‌هزینه‌ترین سفر را برای رساندن بسته‌ها برنامه‌ریزی کند.

• چندین سناریو به عنوان ورودی داده می‌شود. در خط اول هر سناریو ‎$ ‎6‎ $‎ عدد داده شده است. ‎$ ‎n, m‎, ‎A, ‎B, ‎C‎ $‎ و ‎$ ‎D‎ $‎ که ‎$ n‎ ‎(4 \leq n \leq 100)‎ $‎ تعداد فرودگاه‌ها و ‎$ m ‎‎‎(‎0 \leq m \leq 10000‎)‎ $‎ تعداد پروازهای مستقیم و غیر‌مستقیم است که حداکثر ‎$ ‎1000‎ $‎ تای آن‎‌ها پروازهای غیر‌مستقیم است.
• ‎$ ‎i‎ $‎ امین خط از خط بعدی با دو عدد صحیح مثبت ‎‎هزینه ‎$ ‎p_{i} \leq ‎10^{‎6‎}‎ $‎ و ‎$ ‎s_{‎i‎}‎ $‎ (برای پروازهای مستقیم ‎$ ‎1‎ $‎ و پروازهای غیر‌مستقیم بیش‌تر است.) شروع می‌شود.
• ‎$ ‎s_{‎i}+1‎ $‎ عدد نیز در ادامه در هر خط می‌آید که فرودگاه‌های متمایزی هستند که ترتیب فرودگاه‌های این مسیر است. ورودی ‎$‎‎"‎0‎ 0‎ 0‎ 0‎ 0‎ ‎0‎"‎‎‎$‎ با خاتمه می‌یابد.

برای هر سناریو هزینه‌ی‎ ارزان‌ترین سفر را در یک خط چاپ کنید. در صورتی که رساندن یکی از بسته‌ها غیر ممکن است ‎$ ‎"‎Impossible!‎"‎ $‎ را چاپ کنید.

• محدودیت زمان: ۱۰ ثانیه
• محدودیت حافظه: ۲۵۶ مگابایت

• سوال بعد
• سوال قبل