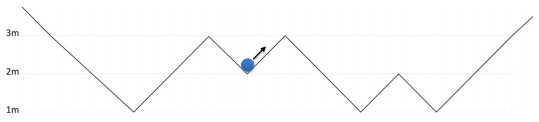
در ‎ ‎‎$ ‎neverland‎ $‎‎‎محدوده‌های کوهستانی بسیاری وجود دارد. هر محدوده کوهستانی شامل تعدادی دره و قله است. شیب بین دو قله و دره‌ی متوالی همواره ‎$ ‎1‎ $‎ و یا ‎$ ‎-1‎ $‎ است و ارتفاع دره‌ها و قله‌ها عدد صحیح است. یک توپ بولینگ در قسمتی از یک محدوده‌ی کوهستانی که شامل ‎$ ‎n‎ $‎ دره و ‎$ ‎n-1‎ $‎ قله است‏، در حال چرخش است. توپ همواره در تماس با سطح کوهستان خواهد بود و پرش نخواهد داشت. ‎‎قبل از اولین دره و بعد از آخرین دره ارتفاع کوهستان به قدری زیاد است که توپ نمی‌تواند از محدوده‌ی کوهستان خارج شود. در زمان ‎$ ‎t_{‎0‎}‎ $‎ توپ در دره شماره ‎$ ‎s‎ $‎ واقع است و جهت آن به سمت بالا-راست و دارای انرژی جنبشی اولیه ‎$ ‎k_{‎0‎}‎ $‎ است. شکل زیر یک محدوده کوهستانی با ‎$ ‎4‎ $‎ دره و ‎$ ‎3‎ $‎ قله را نشان می‌دهد‏، توپ در دومین دره است.(شمارش از چپ به راست است.)

‎بر طبق روابط فیزیک می‌دانیم در زمان توپ دارای انرژی پتانسیل گرانشی ‎$‎p_{t} =‎ ‎mgh‎$‎ و انرژی جنبشی ‎$‎k_t=‎‎(1/2)‎mv^‎2‎$‎ است که ‎$ ‎m‎ $‎ جرم توپ و ثابت گرانش زمین ‎$ ‎g‎ $‎ (برابر با ‎$ ‎10‎ $‎ ) است. ‎$ ‎h‎ $‎ و ‎$ ‎v‎ $‎ به ترتیب ارتفاع و سرعت توپ در زمان ‎$ ‎t‎ $‎ هستند. با تبدیل انرژی پتانسیل به جنبشی و بالعکس مجموع انرژی توپ ‎$‎p_{‎t‎}+‎ ‎k_{‎t‎}$‎ در طول حرکاتش ثابت است مگر اینکه توپ در دره بیافتد.‎‎‎ در دره‌ ‎$i‎$‎ ام‏، ‎$c_i‎‎$‎ واحد از انرژی جنبشی به هدر می‌رود (به خاطر اصطکاک) و یا در صورتی که انرژی جنبشی آن از ‎$c_i$‎ کم‌تر باشد‏، متوقف خواهد شد. (در بقیه مسیر اصطکاک وجود ندارد.) ‎‎توجه کنید که توپ ‎$c_s‎$‎ واحد از انرژی‎‌اش را در هنگام ترک اولین دره در زمان از دست داده است. قطر توپ را ‎$‎0$‎ فرض کنید و جرم آن را ‎$ ‎1‎ $‎ در نظر بگیرید. وظیفه شما پیدا کردن دره و یا قله‌ای است که توپ متوقف خواهد شد.

• سناریوهای مختلفی مختلفی به عنوان ورودی داده خواهد شد. در خط اول هر سناریو عدد صحیح مثبت داده شده است. اولی ‏‎$ n $‎، دومی ‏‎$ ‎s‎ $‎، سومی ‎$ ‎k_{0}‎ $‎ می‌باشد. ‎($1‎ \leq n‎ \leq ‎3000, 1‎\leq s‎‎\leq ‎n, 1‎‎\leq k_0\leq ‎10^5‎‎$)‎
• هر کدام از ‎$ ‎n‎ $‎ خط بعدی شامل ‎$ ‎2‎ $‎ عدد صحیح ‎$ ‎h_i‎‎ $‎ و ‎$ ‎c_{‎i‎}‎ $‎ ارتفاع و اصطکاک دره ‎$ ‎i‎ $‎ ام.
• در ‎$ ‎n-1‎ $‎ خط بعدی نیز ‎$‎H_‎j‎‎$‎ ارتفاع ‎$‎j‎$‎ امین قله داده شده است.(‎$0\leq h_i‎,c_i‎,h_j‎\leq 10^‎9‎$‎) حداقل یکی از ‎$c_i‎s $‎ بزرگ‌تر از صفر است. ورودی با ‎$ ‎"‎0 0 0 0‎"‎ $‎ خاتمه می‌یابد که نباید پردازش گردد.

برای‎ هر سناریو در یک خط جداگانه بر‌اساس اینکه توپ در دره ‎$ ‎valley‎ $‎ و یا قله ‎$ ‎summit‎ $‎ متوقف می‌شود یکی از دو حالت زیر باید چاپ شود.

• اگر توپ در دره شماره ‎$ ‎k‎ $‎ متوقف شد‎‏، ‎$ ‎"Valley: k"‎ $‎ را چاپ کنید‎.‎‎‎
• اگر توپ در ‎‎قله شماره ‎$ ‎k‎ $‎ متوقف شد‏، ‎$ ‎"‎Summit‎: k"‎ $‎ را چاپ کنید‎.‎‎‎

• محدودیت زمان: ۱۰ ثانیه
• محدودیت حافظه: ۲۵۶ مگابایت

• سوال بعد
• سوال قبل