فهرست مندرجات
فاکتوریل
در این صفحه با نماد فاکتوریل آشنا می‌شوید. این نماد، کاربردهای بسیاری در ترکیبیات، به ویژه در ترکیبیات شمارشی دارد.
تعریف
فرض کنید $n$ یک عدد طبیعی باشد. عدد $n!$ ($n$ فاکتوریل) به صورت زیر تعریف می‌شود: $$n! = n \times (n-1) \times (n-2) \times ... \times 1$$
برای مثال: $$5! = 5 \times 4 \times 3 \times 2 \times 1 = 120$$
برای $n=0$ نیز این نماد تعریف می‌شود و به طور قراردادی، $0!=1$ در نظر گرفته می‌شود. این قرارداد شاید در ابتدا عجیب و بیهوده به نظر بیاید، اما انگیزه‌های بسیاری برای تعریف آن وجود دارد که می‌توانید در یک پله بالاتر ببینید.
نماد فاکتوریل تنها به اعداد صحیح نامنفی محدود نمی‌شود و برای دیگر اعداد حقیقی و حتی اعداد غیر حقیقی تعریف می‌شود که می‌توانید در یک پله بالاتر با آن‌ها آشنا شوید.
در جدول زیر می‌توانید چند فاکتوریل ابتدایی را ببینید.
| $n$ | $n!$ |
| 0 | 1 |
| 1 | 1 |
| 2 | 2 |
| 3 | 6 |
| 4 | 24 |
| 5 | 120 |
| 6 | 720 |
| 7 | 5040 |
| 8 | 40320 |
| 9 | 362880 |
| 10 | 3628800 |
| 11 | 39916800 |
| 12 | 479001600 |
| 13 | 6227020800 |
| 14 | 87178291200 |
| 15 | 1307674368000 |
همان طور که مشاهده می‌کنید، با بزرگ شدن $n$، $n!$ رشد بسیاری بالایی دارد.
مثال: درستی یا نادرستی هر یک از موارد زیر را مشخص کنید:
- $$(m+n)!=m!+n!$$
- $$(mn)!=m! \times n!$$
پاسخ
به ازای $m=n=2$، هر دو عبارت داده شده، نادرست می‌شود. پس هر دو عبارت نادرست هستند.
مثال: عبارات زیر را با نماد فاکتوریل، ساده‌تر بنویسید:
- $$(n+1) \times (n+2) \times ... \times (2n)$$
- $$2 \times 4 \times ... \times (2n)$$
- $$1 \times 3 \times ... \times (2n-1)$$
پاسخ
- عبارت بالا را در
$\frac{n!}{n!}$ ضرب می‌کنیم. پس: $$(n+1) \times (n+2) \times ... \times (2n)!$$ $$=(n+1) \times (n+2) \times ... \times (2n)! \times \frac{n!}{n!}$$ $$=\frac{1 \times 2 \times ... \times (2n)}{n!}$$ $$=\frac{(2n)!}{n!}$$
- کافی است به جای هر $2i$، $2 \times i$ بنویسیم.
$$2 \times 4 \times ... \times (2n)$$ $$=(2 \times 1)(2 \times 2)...(2 \times n)$$ $$=2^n \times n!$$
- عبارت قسمت ۲ را $S$ می‌نامیم. عبارت داده شده را در $\frac{S}{S}$ ضرب می‌کنیم. داریم:
$$1 \times 3 \times ... \times (2n-1)$$ $$=1 \times 3 \times ... \times (2n-1) \times \frac{2 \times 4 \times ... \times (2n)}{2 \times 4 \times ... \times (2n)}$$ $$=\frac{(2n)!}{2^n \times n!}$$
فاکتوریل به صورت بازگشتی
با استفاده از تعریف فاکتوریل، نتیجه می‌شود: $$n! = n \times (n-1)!$$
عبارت بالا، یک رابطه‌ی بازگشتی برای $n!$ است. روابط بازگشتی دیگری نیز میتوان برای $n!$ نوشت.
مثال: ثابت کنید: $$n! = (n-1)\big((n-1)! + (n-2)!\big)$$
پاسخ
$$(n-1)\big((n-1)! + (n-2)!\big)$$ $$=(n-1) \times (n-1)! + (n-1) \times (n-2)!$$ $$=(n-1) \times (n-1)! + (n-1)!$$ $$=(n-1)! \times (n-1 + 1)$$ $$=n\times (n-1)!$$ $$=n!$$
چند مثال
مثال: فرض کنید $n, r$ اعدادی طبیعی باشند که $r < n$. ثابت کنید: . ثابت کنید: $$\frac{n!}{r! \times (n-r)!} = \frac{(n-1)!}{r! \times (n-r-1)!} + \frac{(n-1)!}{(r-1)! \times (n-r)!}$$
پاسخ
$$\frac{(n-1)!}{r! \times (n-r-1)!} + \frac{(n-1)!}{(r-1)! \times (n-r)!}$$ $$=\frac{(n-1)! \times \big(n-r + r \big)}{r! \times (n-r)!}$$ $$=\frac{n!}{r! \times (n-r)!}$$
توضیح: این رابطه در مباحث بعدی، بیش‌تر بررسی خواهد شد.
مثال: ثابت کنید توان عامل $k$ در تجریه‌ی $n!$ به عوامل اول، $$\Big\lfloor \frac{n}{k} \Big\rfloor + \Big\lfloor \frac{n}{k^2} \Big\rfloor + \Big\lfloor \frac{n}{k^3} \Big\rfloor + ... $$ است. سپس تعداد ارقام صفر سمت راست عدد $200!$ را به دست بیاورید.
پاسخ
هر عددی از اعداد $1, 2, ..., n$ که بر $k$ بخش‌پذیر هستند، یک عامل $k$ می‌سازد که $\Big\lfloor \frac{n}{k} \Big\rfloor$ آن‌ها را می‌شمارد. هر عددی نیز که بر $k^2$ بخش‌پذیر است، دو عامل $k$ می‌سازد که یکی از آن‌ها در $\Big\lfloor \frac{n}{k} \Big\rfloor$ شمرده شده است و دیگری در
$\Big\lfloor \frac{n}{k^2} \Big\rfloor$ شمرده می‌شود. برای دیگر توان‌های $k$ نیز، به همین ترتیب جلو می‌رویم و حکم اثبات می‌شود.
حال تعداد ارقام صفر سمت راست عدد $200!$ را محاسبه می‌کنیم. باید تعداد عامل‌های ۲ و ۵ را بشماریم. واضح است که توان عامل ۵ کم‌تر از توان عامل ۲ است. پس کافی است توان عامل ۵ را بشماریم. توان عامل ۵ برابر است با: $$\Big\lfloor \frac{200}{5} \Big\rfloor + \Big\lfloor \frac{200}{25} \Big\rfloor + \Big\lfloor \frac{200}{125} \Big\rfloor$$ $$=40 + 8 + 1 = 49$$
مثال: ثابت کنید: $$1 \times 1! + 2 \times 2! + ... + n \times n! = (n+1)! - 1$$
راهنمایی
ابتدا ثابت کنید: $$k \times k! = (k+1)! - k!$$
پاسخ
ابتدا ثابت می‌کنیم: $$k \times k! = (k+1)! - k!$$ داریم: $$k \times k! = k \times k! + k! - k!$$ $$=(k+1) \times k! - k! = (k+1)! - k!$$ حال حکم اصلی را ثابت می‌کنیم: $$1 \times 1! + 2 \times 2! + ... + n \times n!$$ $$=2! - 1! + 3! - 2! + 4! - 3! + ... + (n+1)! - n!$$ $$=(n+1)! - 1$$
مثال: ثابت کنید: $$\frac{1}{(1+1)!} + \frac{2}{(2 + 1)!} + ... + \frac{n}{(n + 1)!}=1 - \frac{1}{(n+1)!}$$
راهنمایی
ابتدا ثابت کنید: $$\frac{k}{(k+1)!} = \frac{1}{k!} - \frac{1}{(k+1)!}$$
پاسخ
ابتدا ثابت می‌کنیم: $$\frac{k}{(k+1)!} = \frac{1}{k!} - \frac{1}{(k+1)!}$$ داریم: $$\frac{1}{k!} - \frac{1}{(k+1)!} = \frac{(k+1)-1}{(k+1)!} = \frac{k}{(k+1)!}$$ حال حکم اصلی را ثابت می‌کنیم: $$\frac{1}{(1+1)!} + \frac{2}{(2 + 1)!} + ... + \frac{n}{(n + 1)!}$$ $$=\frac{1}{1!} - \frac{1}{2!} + \frac{1}{2!} - \frac{1}{3!} + ... + \frac{1}{n!} - \frac{1}{(n+1)!}$$ $$=1 - \frac{1}{(n+1)!}$$
یک پله بالاتر
انگیزه‌های تعریف $0!$
قراردادن مقدار ۱ برای $0!$، انگیزه‌ها و دلایل بسیاری داشته است که برخی از آن‌ها را به طور مختصر مشاهده می‌کنید:
- تعداد جایگشت‌های خطی با ۰ عنصر، برابر با ۱ است، زیرا تنها یک حالت برای جایگشت دادن ۰ عنصر داریم (جایگشت خالی).
- در فرمول ترکیب $\binom{n}{r}$، به ازای $r=0$ و $r=n$، باید مقدار ۱ را ببینیم و این در حالی است که مقدار $0!$ در مخرج فرمول ظاهر می‌شود که اگر آن را برابر ۱ در نظر بگیریم، مشکل حل می‌شود.
- در ریاضیات، مفهومی به نام ضرب تهی وجود دارد که با نوشتن فاکتوریل به صورت بازگشتی، ایجاب می‌کند $0!=1$ باشد.
- فاکتوریل محدود به اعداد صحیح نامنفی نیست و به اعداد حقیقی و حتی اعداد مختلط، تعمیم داده می‌شود. با تعریفی که برای فاکتوریل، در این تعمیم داده می‌شود، $0!=1$ است. این تعمیم را در ادامه‌ی این صفحه خواهید دید.
- در بسیاری از بسط‌های تیلور توابع، ضریب $0!$ ظاهر می‌شود. بسط‌های تیلور در صورتی درست کار می‌کنند که $0!=1$ باشد.
تعمیم به اعداد حقیقی و مختلط
به جز اعداد صحیح منفی، برای بقیه‌ی اعداد حقیقی مانند $x$، عدد $x!$ تعریف می‌شود. ابتدا تابع گاما را تعریف می‌کنیم. فرض کنید $x$ یک عدد حقیقی باشد. هم‌چنین فرض کنید $x$ یک عدد صحیح نامثبت نیست. در این صورت تابع $\Gamma (x)$ به صورت زیر تعریف می‌شود: $$\Gamma (x) = \int_{0}^{\infty}t^{x-1}e^{-t}dt$$ حال فرض کنید $x$, یک عدد حقیقی باشد. هم‌چنین فرض کنید $x$ یک عدد صحیح منفی نیست. در این صورت $x!$ به صورت زیر تعریف می‌شود: $$x! = \Gamma (x+1)$$
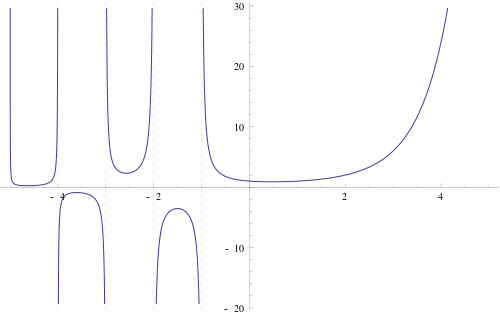
نمودار تابع $y=x!$ را در شکل زیر مشاهده می‌کنید:
تابع گاما این خاصیت را دارد که: $$\frac{\Gamma (n+1)}{\Gamma (n)} = n$$ پس طبیعی است که تابع گاما برای $n=0$ تعریف نشود. وقتی برای $n=0$ تعریف نشود، برای $n=-1$ نیز تعریف نمی‌شود و به همین ترتیب برای دیگر اعداد صحیح نامثبت نیز تعریف نخواهد شد. پس نتیجه می‌شود تابع $x!$ برای اعداد صحیح منفی تعریف نشود.
با توجه به این که، تابع گاما این قابلیت را دارد که برای اعداد مختلط تعریف شود، تابع $y=x!$ می‌تواند به اعداد مختلط تعمیم داده شود. فرض کنید $z = a + bi$، یک عدد مختلط باشد. در این صورت داریم: $$z! = \Gamma (a + bi + 1)$$
کاربرد در نظریه اعداد
اعداد فاکتوریل، خاصیت‌های جالبی در نظریه اعداد دارند که دو مورد از آن‌ها به طور مختصر در زیر آمده است:
- به ازای هر عدد طبیعی $n$ که $n>5$، عدد $n$ عددی مرکب است، اگر و تنها اگر $$(n-1)! \equiv 0 \pmod{n}$$.
- قضیه‌ی ویلسون: عدد طبیعی $p$ اول است، اگر و تنها اگر $$(p-1)! \equiv -1 \pmod{p}$$.
چند خاصیت جالب
فاکتوریل خواص جالب دیگری نیز دارد که برخی از آن‌ها در زیر به طور مختصر آمده است:
- با نوشتن بسط تیلور $e^1$ داریم: $$\frac{1}{0!}+\frac{1}{1!}+\frac{1}{2!}+... = e$$
- با بردن $n$ به سمت بی‌نهایت در عبارت $$\frac{1}{2!}+\frac{2}{3!}+\frac{3}{4!} + ... + \frac{n}{(n+1)!} = 1 - \frac{1}{(n+1)!}$$ که در مثال‌ها بررسی شد، داریم: $$\frac{1}{2!}+\frac{2}{3!}+\frac{3}{4!}+... = 1$$
- $$(-\frac{1}{2})! = \sqrt{\pi}$$
- در بحث تحلیل پیچیدگی الگوریتم‌ها و محاسبه‌ی $O$، $\Omega$ و $\theta$ توابع، میتوان گفت: $$lg(n!) \in \theta(n \times lg(n))$$ این خاصیت در تحلیل پیچیدگی بسیاری از الگوریتم‌ها مانند الگوریتم‌های مرتب‌سازی مقایسه‌ای، کاربرد دارد.
منابع و مراجع
- Chen Chuan-Chong, Koh Khee-Meng (1992), Principles and Techniques in Combinatorics, Singapore, World Scientific
خواننده‌ی گرامی، لطفا در صورت داشتن پیشنهاد یا مشاهده‌ی مشکل (علمی، تایپی و …) در این صفحه، به ما اطلاع دهید:
ابزار صفحه
کلیه‌ی حقوق این سایت متعلق به کمیته‌ی ملی المپیاد کامپیوتر ایران است.
نظرات
با سلام . با استفاده از 26 حرف زبان انگلیسی میخواهیم تعدادی عبارت سه حرفی بسازیم .چند عبارت سه حرفی میتوان ساخت؟
ممنون
با عرض سلام و خسته نباشید. در فهرست های اموزش المپیاد مثل ترکیبیات چرا ان هایی قرمز رنگ هستند در صفحه وجود ندارند؟ با تشکر
لینک‌ها قرمزرنگ نشانگر صفحاتی است که هنوز مطلبی در آن‌ها درج نشده است.