فهرست مندرجات
اصل متمم
اصل متمم، یکی دیگر از اصول اولیه‌ی شمارش است. این اصل، روشی است که گاهی می‌تواند برای جلوگیری از حالت‌بندی‌های زیاد، به کار رود. در این اصل، به جای شمردن حالات مطلوب، حالات نامطلوب را می‌شماریم.
یک مثال
مثال زیر را در نظر بگیرید:
مثال: در چند عدد ۴ رقمی، رقم تکراری وجود دارد؟
پاسخ
اگر بخواهیم با اصل جمع و حالت‌بندی مسئله را حل کنیم، حالت‌بندی ما بسیار سخت و طولانی خواهد شد. بنابراین بهتر است روشی دیگر انتخاب کنیم.
ابتدا با اصل ضرب، تعداد اعداد ۴ رقمی که رقم تکراری ندارند را می‌شماریم. رقم سمت چپ، ۹ حالت دارد (۰ نمی‌تواند باشد). رقم بعدی ۹ حالت دارد (برابر رقم اول نمی‌تواند باشد). به همین ترتیب ۲ رقم دیگر به ترتیب ۸ و ۷ حالت دارند. پس در کل $9\times9\times8\times7$ عدد ۴ رقمی وجود دارند که رقم تکراری نداشته باشند. از طرفی می‌دانیم تعداد کل اعداد ۴ رقمی، ۹۰۰۰ تاست. پس پاسخ برابر $9000 - 9\times9\times8\times7$ است.
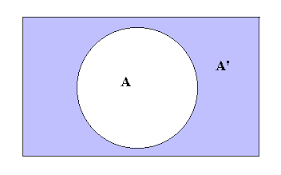
تعریف اصل متمم
فرض کنید $A$ زیرمجموعه‌ای از مجموعه‌ی مرجع $M$ باشد. اصل متمم می‌گوید تعداد اعضایی که در $A$ قرار ندارند (تعداد اعضای $A'$)، برابر $|M|-|A|$ است. در واقع:
$$|A'|=|M|-|A|$$
سایر مثال‌ها
توجه: سعی کنید ابتدا خودتان روی مسائل به قدر کافی فکر کنید و سپس به پاسخ مراجعه کنید.
مثال: فرض کنید $a, b$ اعدادی طبیعی هستند. تعداد اعداد مجموعه‌ی $\{a, a + 1, ..., b\}$ چند تاست؟
پاسخ
شاید در نگاه اول بگوییم پاسخ $b-a$ است، اما این طور نیست. مجموعه‌های $M=\{1, 2, ..., b\}$ و $A=\{1, 2, ..., a-1\}$ را در نظر بگیرید. طبق اصل متمم، پاسخ برابر $|M|-|A|=b-a+1$ است.
مثال: در چند زیرمجموعه از مجموعه‌ی $\{1, 2, ..., 2n\}$ عدد زوج، وجود دارد؟
پاسخ
تعداد کل زیرمجموعه‌های مجموعه، طبق بخش‌های قبل، $2^{2n}$ است. از طرفی تعداد زیرمجموعه‌هایی که عدد زوج ندارند، $2^n$ تاست (هر عدد فرد به ۲ حالت می‌تواند در زیرمجموعه باشد یا نباشد و اعداد زوج هم به ۱ حالت نباید در زیرمجموعه باشند). پس طبق اصل متمم، پاسخ برابر $2^{2n}-2^n$ است.
مثال: اعداد طبیعی $n, m$ را در نظر بگیرید. فرض کنید تجزیه‌ی عدد $n$ به عوامل اول، به صورت $n=p_1^{a_1} p_2^{a_2} ... p_k^{a_k}$ باشد. اگر در تجزیه‌ی $m$ به عوامل اول، توان عامل $p_i$، برابر $b_i$ باشد ($0 \le b_i \le a_i$) ، تعداد مقسوم‌علیه‌های مثبت عدد $n$ که بر $m$ بخش‌پذیر نیستند، چقدر است؟
پاسخ
ابتدا تعداد مقسوم‌علیه‌های مثبت عدد $n$ را می‌شماریم که بر $m$ بخش‌پذیر هستند. برای این کار، همان روشی را در نظر می‌گیریم که در اصل ضرب به کار گرفتیم. توان عامل $p_i$ در چنین مقسوم‌علیهی، باید بیش‌تر مساوی $b_i$ و کم‌تر مساوی $a_i$ باشد؛ پس $a_i-b_i+1$ حالت دارد. پس تعداد این مقسوم‌علیه‌ها، $$(a_1-b_1+1)(a_2-b_2+1)...(a_k-b_k+1)=\prod_{i=1}^{k}(a_i-b_i+1)$$ است.
از طرفی طبق بخش‌های قبل، تعداد کل مقسوم‌علیه‌های مثبت عدد $n$ برابر $$(p_1+1)(p_2+1)...(p_k+1)=\prod_{i=1}^{k}(a_i+1)$$ است.
پس طبق اصل متمم، پاسخ برابر $$\prod_{i=1}^{k}(a_i+1) - \prod_{i=1}^{k}(a_i-b_i+1)$$ است.
مسائل نمونه
ابزار صفحه
کلیه‌ی حقوق این سایت متعلق به کمیته‌ی ملی المپیاد کامپیوتر ایران است.
