فهرست مندرجات
اصل جمع
اصل جمع همانند اصل ضرب، یکی دیگر از اصول اولیه‌ی شمارش است.
یک مثال
مثال: فرض کنید شما برای انجام کاری، در بیرون از خانه هستید و مجبورید ناهار خود را از بیرون تهیه کنید. در اطراف شما یک رستوران ایرانی با ۵ نوع غذا و یک فست‌فود با ۳ نوع غذا وجود دارد. شما به چند طریق می‌توانید غذای امروز خود را تهیه کنید؟
غذای ما یا از رستوران ایرانی تهیه خواهد شد یا از فست‌فود؛ پس $5+3=8$ روش برای انجام این کار وجود دارد.
تعریف
اصل جمع در ریاضیات به صورت زیر تعریف می‌شود:
اگر کاری به $a$ طریق و کاری دیگر به $b$ طریق قابل انجام باشد، تعداد روش‌های انجام دادن یکی از این دو کار، $a+b$ است.
مثال:
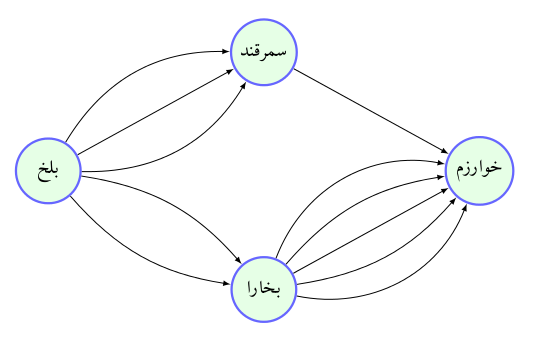
جاده‌های بین شهرهای سمرقند، بخارا، بلخ و خوارزم، به شکل زیر است. به چند روش می‌توان از شهر بلخ، به شهر خوارزم رفت؟
راهنمایی
از اصل ضرب نیز کمک بگیرید.
پاسخ
برای رفتن از بلخ به خوارزم، یا باید باید از شهر میانی سمرقند استفاده کنیم، یا باید از شهر میانی بخارا بهره ببریم. اگر از شهر میانی سمرقند استفاده کنیم، طبق اصل ضرب $3\times 1$ حالت و اگر از شهر میانی بخارا استفاده کنیم، طبق اصل ضرب، $2\times 5$ حالت داریم. پس طبق اصل جمع، پاسخ برابر $3+10=13$ است.
تعمیم
گوییم مجموعه‌ی $A$ به زیرمجموعه‌های ناتهی $A_1, A_2, ..., A_n$ افراز شده است، اگر $A_1\cup{}A_2\cup{}...\cup{}A_n=A$ و به ازای هر $1\le{}i<j\le{}n$ داشته باشیم $A_i\cap{}A_j=\phi$. در واقع به زبان خودمانی، مجموعه‌ی $A$ را به $n$ زیرمجموعه‌ی ناتهی، تقسیم کرده‌ایم.
اصل جمع در ریاضیات به صورت زیر بیان می‌شود: فرض کنید مجموعه‌ی $A$ به $n$ زیرمجموعه‌ی $A_1, A_2, ..., A_n$ افراز شده باشد. آن‌گاه داریم $$|A_1|+|A_2|+...+|A_n|=\sum_{i=1}^{n}|A_i|=|A|$$
در واقع استفاده از اصل جمع، همان تقسیم مسئله به حالت‌های مختلف یا حالت‌بندی است. هر کجا می‌خواهیم حالت‌بندی کنیم، در واقع داریم از اصل جمع استفاده می‌کنیم. یک حالت‌بندی خوب، باید ویژگی‌های زیر را داشته باشد:
- تمام حالات ممکن را پوشش دهد. در یک حالت‌بندی خوب، نباید حالت یا حالاتی از قلم بیفتد و محاسبه نشود.
- حالات مسئله را به درستی افراز کند. در یک حالت‌بندی درست، نباید حالت یا حالاتی وجود داشته باشد که ما آن‌ها را دو یا چند بار می‌شماریم.
- تعداد حالت‌هایی که مسئله را به آن‌ها می‌شکنیم، کم باشد. هر چه حالت‌بندی ما پیچیده‌تر و طولانی‌تر باشد، احتمال خطا و اشتباه، بالاتر می‌رود.
مثال:
چند مثال
توجه: سعی کنید ابتدا خودتان روی مسائل به قدر کافی فکر کنید و سپس به پاسخ مراجعه کنید.
مثال: چند عدد ۲ رقمی زوج با ارقام متمایز داریم؟
پاسخ
بیایید مانند روش اصل ضرب، جلو برویم. رقم یکان ۵ حالت دارد (باید زوج باشد). برای تعیین رقم دهگان به مشکل برمی‌خوریم. اگر رقم یکان ۰ باشد، رقم دهگان ۹ حالت دارد (۰ نمی‌تواند باشد) و اگر رقم یکان غیر ۰ باشد، رقم دهگان ۸ حالت دارد (۰ و رقم یکان نمی‌تواند باشد). پس این‌جا باید از اصل جمع استفاده کنیم و حالت‌بندی کنیم. پس اعداد را به ۲ دسته تقسیم می‌کنیم:
- رقم یکان ۰ باشد: در این حالت رقم دهگان ۹ حالت دارد. پس تعداد اعداد این حالت $9\times1=9$ است.
- رقم یکان غیر ۰ باشد: در این حالت رقم یکان ۴ حالت دارد و رقم دهگان ۸ حالت دارد. پس تعداد اعداد این حالت $8\times4=32$ است.
پس در کل طبق اصل جمع، پاسخ برابر $9+32=41$ است.
مثال: فرض کنید وارد یک رستوران شده‌اید. در این رستوران غذاهای چلوکباب، جوجه‌کباب، قرمه‌سبزی، پیتزا مخصوص و همبرگر و نوشیدنی‌های نوشابه، دوغ، دلستر و آبمیوه وجود دارد. در این رستوران غذاهای ایرانی تنها با نوشابه و دوغ و غذاهای فست‌فود تنها با نوشابه و دلستر و آبمیوه می‌توانند صرف شوند. شما به چند طریق می‌توانید غذای خود را در این رستوران تهیه کنید؟
پاسخ
باز هم مسئله را به ۲ حالت تقسیم می‌کنیم:
- اگر غذای ایرانی تهیه کنیم، ۲ حالت برای نوشیدنی وجود دارد. پس $3\times2=6$ حالت داریم.
- اگر فست‌فود تهیه کنیم، ۳ حالت برای نوشیدنی وجود دارد. پس $2\times3=6$ حالت داریم.
پس در کل طبق اصل جمع، پاسخ برابر $6+6=12$ است.
مثال: به چند روش می‌توان خانه‌های یک جدول $2\times2$ را با ۳ رنگ، رنگ‌آمیزی کرد؛ طوری که هیچ دو خانه‌ی مجاور هم‌رنگ نباشند؟ توجه کنید به ۲ خانه مجاور گوییم، اگر یک ضلع مشترک داشته باشند.
پاسخ
خانه‌های بالا-چپ، بالا-راست، پایین-چپ و پایین-راست جدول را به ترتیب با خانه‌های ۱، ۲، ۳ و ۴ شماره‌گذاری می‌کنیم. خانه‌ی ۱، ۳ حالت برای رنگ‌آمیزی دارد. حال مسئله را ۲ حالت می‌کنیم:
- خانه‌های ۲ و ۳ هم‌رنگ باشند: در این حالت رنگ خانه‌های ۲ و ۳، ۲ حالت دارد و رنگ خانه‌ی ۴، ۲ حالت دارد (باید متفاوت با رنگ خانه‌های ۲ و ۳ باشد). پس $3\times2\times2=12$ حالت داریم.
- خانه‌های ۲ و ۳ هم‌رنگ نباشند: در این حالت رنگ خانه‌ی ۲، ۲ حالت دارد و سپس رنگ خانه‌ی ۳ یکتا تعیین می‌شود (رنگی که نه در خانه‌ی ۱ و نه در خانه‌ی ۲ آمده است). رنگ خانه‌ی ۴ نیز یکتا تعیین می‌شود (رنگی که نه در خانه‌ی ۲ و نه در خانه‌ی ۳ آمده است). پس $3\times2\times1\times1=6$ حالت داریم.
پس در کل طبق اصل جمع، پاسخ برابر $12+6=18$ است.
مثال: فرض کنید در صفحه‌ی مختصات می‌خواهید از نقطه‌ی $(0, 0)$ به نقطه‌ی $(2,2)$ بروید و در هر حرکت می‌توانید یک واحد به بالا یا یک واحد به راست بروید. چند مسیر برای این کار وجود دارد؟
پاسخ
تعداد روش‌های رفتن از خانه‌ی $(0, 0)$ به خانه‌ی $(a, b)$ را $f(a, b)$ می‌نامیم. در واقع ما می‌خواهیم $f(2,2)$ را پیدا کنیم. فرض کنید ما $f(x, y-1)$ و $f(x-1,y)$ را می‌دانیم. حال می‌خواهیم $f(x, y)$ را پیدا کنیم. مسیرهایی که به نقطه‌ی $(x, y)$ می‌رسند، ۲ حالت دارند: یا از نقطه‌ی $(x, y-1)$ آمده‌اند یا از نقطه‌ی $(x-1, y)$. پس طبق اصل جمع $f(x, y)=f(x, y-1)+f(x-1, y)$.
از طرفی به وضوح $f(0, 0)=f(0, 1)=f(0, 2)=f(1, 0)=f(2, 0)=1$. پس به دست می‌آید:
$$f(1, 1)=f(1, 0)+f(0,1)=2$$ $$f(1, 2)=f(1,1)+f(0,2)=3$$ $$f(2, 1)=f(2,0)+f(1,1)=3$$ $$f(2, 2)=f(2,1)+f(1,2)=6$$
پس پاسخ ۶ است. در مباحث بعدی، پاسخ‌های ساده‌تری برای چنین مسائلی خواهید یافت.
مسائل نمونه از المپیادهای کامپیوتر ایران
منابع و مراجع
ابزار صفحه
کلیه‌ی حقوق این سایت متعلق به کمیته‌ی ملی المپیاد کامپیوتر ایران است.
