سوالات ۲۷ و ۲۸ و ۲۹ و ۳۰ و ۳۱
امین٬ علی٬ محمد٬ مصطفی و مهدی در یک اتاق نشسته اند. هر یک از آنها به طور ثابت به دقیقا یک نفر دیگر نگاه می کنند و البته متوجه می شوند که او نیز به چه کسی نگاه می کند.
مرتضی وارد اتاق می شود و از هریک از آنها دو سوال می پرسد:
(آ) در لحظهي ورود من به اتاق چه کسی را می دیدی؟
(ب) فردی که به او نگاه می کردی٬ چه کسی را می دید؟
او $۲\times ۵ = ۱۰ $ پاسخ میشنود و آنها را در یک جدول $۲\times ۵ $ به صورت زیر تنظیم می کند:
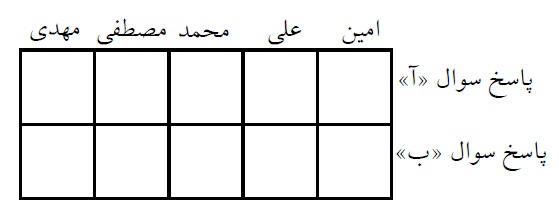
با توجه به توضیحات بالا به ۵ سوال زیر پاسخ دهید (فرض های هر سوال مستقل از سایر سوالهااست):
سوال ۲۷
اگر همه افراد پاسخ درستی بدهند جدول مرتضی به چند حالت مختلف ممکن می تواند پر شود؟
- $۲^{۱۰}$
- !۵
- $۲۰^۵$
- ۴۴
- $۵^۵$
پاسخ
گزینهی «۱» درست است.
اولا که میتوان این سوال را با گراف متناظر کرد به این صورت که میگوییم یک گراف 5 راسی داریم و هر راس آن یک یال خروجی دارد، البته در این سوال نیازی به این تبدیل نیست اما ممکن است شهود شما را برای حل این مسئله بهتر کند.
برای شمردن همه حالات کافیست پاسخ (آ) هر نفر را پر کنیم سپس پاسخ های (ب) آنها یکتا معلوم میشود. پس میشود: $4^5$
سوال ۲۸
مرتضی جدولی را که در آن تنها نام دو نفر به چشم بخورد٬ یک «جدول دونفره» مینامد! چند تا از جدول های معتبر و ممکن٬ «دو نفره» هستند؟
- ۳۲
- ۱۰
- ۸۰
- ۸
- ۳۲۰
پاسخ
گزینهی «۳» درست است.
پس اگر بخواهیم نام دو نفر در این جدول باشد باید اولا این دو نفر به هم نگاه کنند و ثانیا بقیه هم همه به یکی از این دو نگاه کنند. پس کل حالات میشود: $\binom{5}{2}\times2^3 = 80$
سوال ۲۹
فرض کنید مهدی از پاسخ دادن به سوالات طفره رفته است. با این حال مرتضی با بررسی پاسخ دیگران موفق می شود ستون مربوط به پاسخ مهدی را پر کند. چند تا از جدول های ممکن مرتضی این ویژگی را دارند که بتوان با خالی بودن پاسخ مهدی٬ مقدار آن خانه را به طور یکتا استنباط کرد؟
- ۹۴۳
- ۱۷۵
- ۸۱
- ۳۶۹
- ۷۰۰
پاسخ
گزینهی «۵» درست است.
شرط لازم و کافی در این سوال این است که حداقل یک نفر باشد که به مهدی نگاه کند. از آنجا که ممکن است شماردن این حالات کمی مشکل باشد با استفاده از اصل متمم حالتهای قرینه این سوال ( یعنی کسی نباشد که مهدی را ببیند) را میشماریم و از کل کم میکنیم. پس هر کسی به هرکس دیگر بهجز مهدی میتواند نگاه کند. پس جواب میشود :$4^5- (4\times3^4)=700$
سوال ۳۰
مرتضی جدول معتبری که بتوان با دانستن هر چهار ستون آن جدول٬ ستون پنجم را به طور دقیق و یکتا استنباط کرد٬ یک جدول «رویایی» مینامد. چند تا از جدول های ممکن رویایی هستند؟
- ۲۴
- ۱۲۰
- ۴۴
- ۳۲
- ۶
پاسخ
گزینهی «۳» درست است.
شرط لازم و کافی برای یک جدول رویایی این است که هر کسی را حداقل یک نفر دیگر ببیند و چون هرکس هم یک نفر را میبیند پس هرکس را دقیقا یک نفر میبیند. حال اگر یک جایشگت از 1 تا 5 در نظر بگیرید، میگوییم نفر $i$ ام ، $i$ امین نفر در جایشگت را میدیده است. حال میتوان این مسئله را با مسئله تعداد پرشها در جایگشتها یکی دانست یعنی میخواهیم تعداد جایگشتهایی را پیدا کنیم که هیچ عددی سر جای خودش نباشد. برای اطلاعات بیشتر می توانید به این لینک مراجعه کنید که با اصل متمم و شمول و عدم شمول به این رابطه میرسیم : $n!× ∑_0^n\frac{(-1)^n}{i!}$
همچنین این مسئله راه حل ساده تری هم دارد به اینطریق که اگر این مسئله را به گراف تبدیل کرده باشیم میفهمیم که یا یک دور به طول 3 و یک دور به طول 2 دارد یا کلا یک دور به طول 5 است.
که یعنی میشود : $4!+ \binom{5}{2}×2!=44$
سوال ۳۱
فرض کنید یکی از این پنج نفر به حداقل یک سوال٬ پاسخ اشتباه داده است ولی بقیه راست گو هستند. مرتضی می خواهد از روی پاسخ ها فرد دروغ گو را پیدا کند. می دانیم پاسخ های امین به این صورت است:
(آ) علی را می دیدم.
(ب) علی محمد را می دید.
چند تا از گزاره های زیر درست هستند؟
- اگر امین دروغ گو باشد مرتضی او را پیدا می کند.
- اگر علی دروغ گو باشد مرتضی او را پیدا می کند.
- اگر محمد دروغ گو باشد مرتضی او را پیدا می کند.
- اگر مصطفی یا مهدی دروغ گو باشند مرتضی آنها را پیدا می کند.
- ۱
- ۲
- ۴
- ۰
- ۳
پاسخ
گزینهی «۴» درست است.
اگر توجه کنید تمام گزینههای به این صورت است که اگر $v$ دروغگو باشد مرتضی او را پیدا میکند.
بیایید بررسی کنیم در چه صورتی مرتضی میتواند کسی را پیدا کند؟ در صورتی که کسی پرسش اولش جواب غلط داده باشد و پرسش دوم را درست گفته باشد، تنها در صورتی لو میرود که حداقل 2 نفر دیگر نیز او را نگاه کرده باشند. پس اگر دو نفر حرفهایشان تناقض داشت و هیچ دو نفری نبودند که به یکی از این دو نفر نگاه کنند، ما نمیتوانیم به گفته هیچ یک اعتماد کنیم و در نتیجه نمیتوانیم دروغگو را پیدا کنیم. بنابراین میتوانید برای هرکدام از حالت ها مثال نقضی پیدا کنید، پس جواب 0 میشود.

