سوال ۳۰
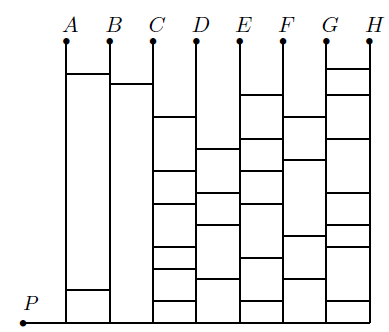
نقشهی خیابانهای یک شهر مانند شکل روبرو است. خیابانهای عمودی به سمت بالا یکطرفه و خیابانهای افقی دوطرفه هستند. در هر یک از نقاط A تا H یک پارکینگ قرار دارد. شخصی با اتومبیل خود از نقطه P به حرکت در میآید. با فرض اینکه این شخص از هیچ نقطهای بیش از یک بار عبور نمیکند، تعداد راههای رسیدن او به هر یک از نقاط A تا H را به ترتیب W_A تا W_H مینامیم. مقدار W_A - W_B - W_C + W_D + W_E – W_F – W_G + W_H کدام یک از گزینههای زیر است؟
- ۲-
- ۱-
- ۰
- ۲
- هیچکدام
پاسخ
گزینهی (۱) درست است.
ثابت میکنیم:
W_A=W_B,W_C=W_D+2,W_E=W_F,W_G=W_H
برای دو نقطه مثل A,B اگر بالاترین خیابان هرکدام از این ستونها، خیابان بین این دو باشد تناظری یک به یک بین مسیرهای منتهی به این نقاط وجود دارد. چرا که برای رسیدن به این نقاط باید به ارتفاع خیابان بین این دو برسیم و در این حالت به ازای هر مسیر به A یک مسیر نیز به B وجود دارد. در نتیجه تعداد مسیرهای منتهی به این نقاط با یکدیگر برابرند. این استدلال برای زوج نقاط E,F و G,H نیز درست است. ولی برای نقاط C,D شرایط فرق میکند. اگر فرض کنیم خیابان بین B و C وجود ندارد بقیه مسیرها با هم متناظر هستند. پس کافیست که تنها مسیرهایی را محاسبه کنیم که از این خیابان استفاده میکنند و به C ختم میشوند. با توجه به اینکه تنها میتوان به سمت بالا، چپ و راست حرکت کرد تنها دو مسیر با این ویژگی وجود دارد. پس مجموع یاد شده در مسئله برابر با (2-) است.

