سوالات المپیاد:مرحله ی دوم:دوره ی ۲۹:سوالات ۱۴ و ۱۵
فهرست مندرجات
سوالات ۱۴ و ۱۵
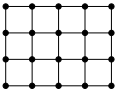
فرض کنید یک جدول $m \times n$ داریم. نقاط گوشههای مربعهای واحد جدول را رأس و اضلاع آنها را یال در نظر بگیرید؛ به این ترتیب یک گراف به دست میآید. برای مثال به ازای $m=3$ و $n=4$ گرافی با ۲۰ رأس و ۳۱~یال به شکل زیر به دست میآید:
به این گراف، گراف جدولی حاصل از یک جدول $m \times n$ گوییم. فرض کنید $G$ یک گراف جدولی و $T$ یک زیردرخت فراگیر از آن باشد. به ازای هر خانه از جدول، تعداد یالهایی از $T$ را که ضلع آن خانه هستند، استحکام آن خانه مینامیم.
سوال ۱۴
به ازای $m=10$ و $n=10$، کمینهی مجموع استحکام خانهها را در میان تمام زیردرختهای فراگیر ممکن بیابید.
- 201
- 199
- 120
- 139
- 240
پاسخ
گزینه (1) درست است.