مسابقه‌ی بین‌المللی ربات‌ها قرار هست در تهران برگزار شود. در این مسابقه ربات‌ها باید مسیری را که از پیش تعیین شده است را از ابتدا تا انتها طی کنند.

یک ایستگاه شارژ الکترونیکی (ECC) بر روی مسیر وجود دارد که در آن ربات‌ها می‌توانند باطری خود را شارژ کنند. هر ربات دستگاهی دارد که فاصله ربات تا ECC را گزارش می‌کند. متاسفانه این دستگاه به جای آنکه فاصله‌ی باقی‌مانده روی مسیر تا ECC را نشان دهد فاصله‌ی اقلیدسی ربات تا ECC را نشان می‌دهد.

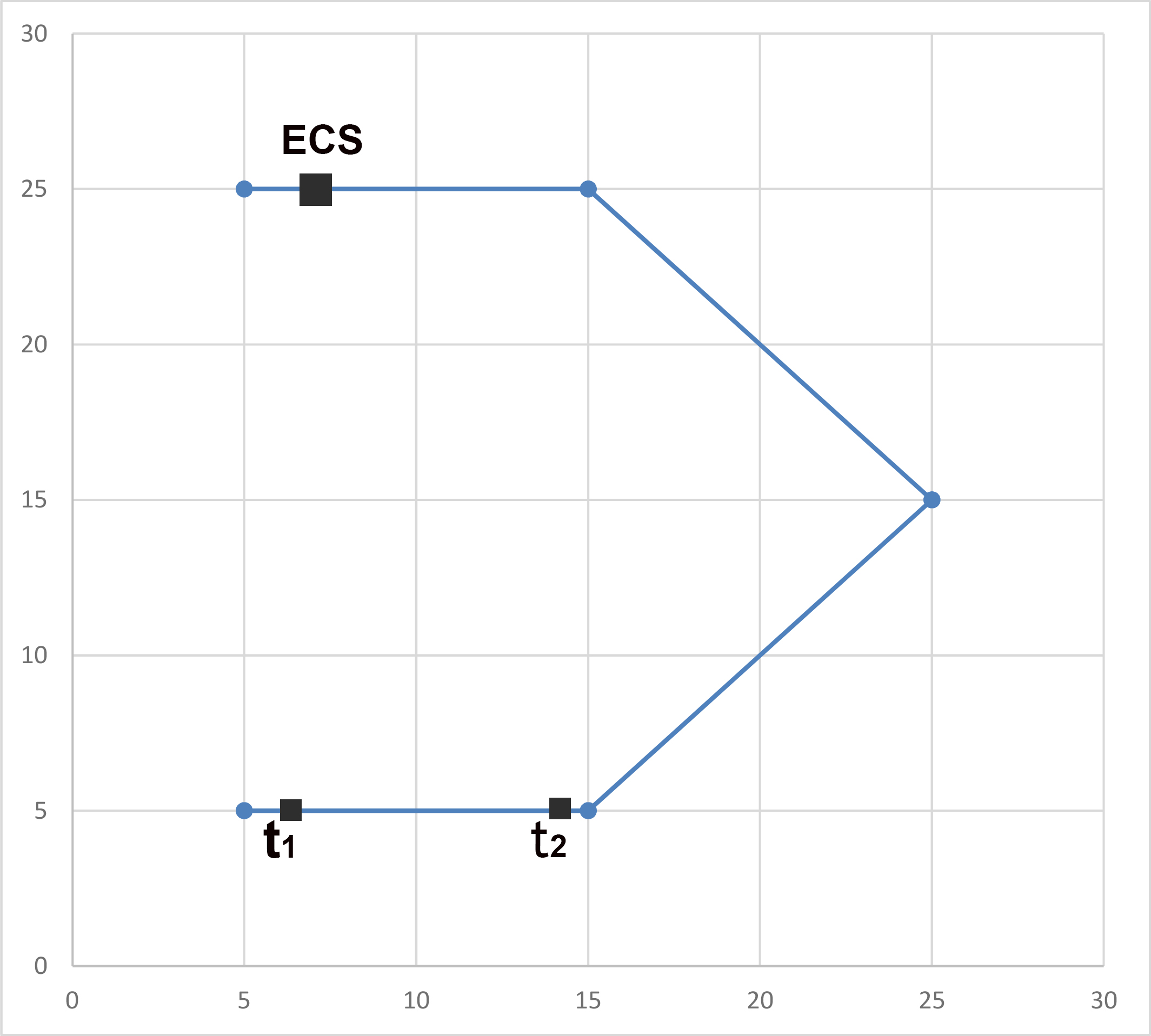
کامران یکی از اعضای کمیته علمی مسابقات است. او می‌داند که یک نقص مشترک در نرم‌افزار کنترلی تعدادی از ربات‌ها وجود دارد. این ربات‌های معیوب تصور می‌کنند که دستگاه‌شان فاصله باقی‌مانده روی مسیر تا ECC را نشان می‌دهد نه فاصله اقلیدسی تا ECC. در نتیجه از نظر این ربات‌ها دستگاه تا قبل از رسیدن به ECC باید یک دنباله‌ی نزولی از اعداد را نشان دهد. اگر چنین نشود، ربات معیوب از کار می‌افتد چرا که تصور می‌کند از کنار ECC بدون آنکه در آن برای شارژ باطری بایستد گذر کرده است. از نظر کامران یک مسیر ناعادلانه است اگر او بتواند ECC را در نقطه‌ای از مسیر نصب کند که ربات‌های معیوب از کار بیافتند. به‌عبارت دیگر، یک مسیر ناعادلانه است اگر موقعیت ECC چنان تعیین شود که سه زمان $t_1 < t_2 < t_3$ وجود داشته باشد که ربات در زمان $t_3$ در ECC باشد و $|p_{t_1}p_{t_3}| < |p_{t_2}p_{t_3}|$ که $|ab|$ نشان‌دهنده فاصله اقلیدسی بین $a$ و $b$ است و $p_t$ موقعیت ربات در زمان $t$ است. کمیته علمی یک لیست از مسیرها را برای مسابقه پیشنهاد کرده است و کامران می‌خواهد مسیری را انتخاب کند که عادلانه باشد (یعنی ناعادلانه نباشد).

در ورودی چند سناریو وجود دارد. در خط اول هر سناریو عدد مثبت صحیح $n$ ($n \leq 10^4$) آمده است که نشان‌دهنده تعداد راس‌های مسیر است. در خط بعد، در هر خط یک جفت عدد صحیح $x$ و $y$ ($-10^6 \leq x,y \leq 10^6$) آمده است. $i$امین جفت $i$امین راس مسیر را مشخص می‌کند. ربات باید از راس اول شروع کرده و از پاره‌خط‌های که راس‌های متوالی را به هم وصل می‌کند گذر کرده و خود را به راس آخر برساند. تضمین می‌شود که مسیر خودش را قطع نمی‌کند. ورودی با 0 تمام می‌شود که نیازی به پردازش آن نیست.

برای هر سناریو در یک خط، وابسته به عادلانه یا ناعادلانه بودن مسیر به‌ترتیب Fair یا Unfair چاپ کنید.

• محدودیت زمان: ۱۰ ثانیه
• محدودیت حافظه: ۲۵۶ مگابایت

• سوال بعد
• سوال قبل