ﯾﮏ ﮐﺎﺷﯽ ﺑﻪ ﻣﺠﻤﻮﻋﻪﺍﯼ ﺍﺯ ﺧﺎﻧﻪﻫﺎﯼ ﯾﮏ ﺟﺪﻭﻝ $h'\times w'$ ﮔﻔﺘﻪ ﻣﯽﺷﻮﺩ. ﺧﺎﻧﻪﻫﺎﯼ ﻫﺮ ﮐﺎﺷﯽ ﻫﻤﺒﻨﺪ ﺍﻧﺪ. ﺑﻪ ﻋﺒﺎﺭﺕ ﺩﯾﮕﺮ ﺭﺥ ﺷﻄﺮﻧﺞ ﻣﯽﺗﻮﺍﻧﺪ ﺍﺯ ﻫﺮ خانه‌ی یک کاشی به هر خانه‌ی دیگر آن برود و تنها از خانه‌های کاشی عبور کند.

ﺑﻪ ﻭﺣﯿﺪ ﮐﺎﺷﯽﮐﺎﺭ، $k$ تا کاشی یکسان داده‌اند و گفته‌اند «ﺁﯼ ﻭﺣﯿﺪ! ﺗﺎ ﺷﺐ ﺍﯾﻦ ﮐﺎﺷﯽﻫﺎ ﺭﺍ ﺩﺭ یک جدول $h \times w$ بچین. ﻧﻪ ﻣﯽﺗﻮﺍﻧﯽ ﮐﺎﺷﯽﻫﺎ ﺭﺍ ﺑﭽﺮﺧﺎﻧﯽ، ﻧﻪ ﻣﯽﺗﻮﺍﻧﯽ ﺷﮑﻞﻫﺎﯼ ﻧﺎﻫﻤﺒﻨﺪ ﺑﺴﺎﺯﯼ ﻭ ﻧﻪ ﺁﻧﻬﺎ ﺭﺍ ﺭﻭﯼ ﻫﻢ ﺑﮕﺬﺍﺭﯼ. ﺑﺒﯿﻨﯿﻢ ﭼﻨﺪ ﺗﺎ ﺷﮑﻞ ﻣﯽﺗﻮﺍﻧﯽ ﺑﺴﺎﺯﯼ. ﺑﺠﻨﺐ!»

ﺍﺯ ﺁﻧﺠﺎ ﮐﻪ ﻭﺣﯿﺪ ﺩﺭ ﺑﭽﮕﯽ ﺑﺮﺍﯼ ﺍﻟﻤﭙﯿﺎﺩ ﺗﻤﺮﯾﻦ ﻣﯽﮐﺮﺩ، ﻓﻬﻤﯿﺪ ﮐﻪ ﺍﮔﺮ ﺩﻭ ﺷﮑﻞ ﺑﺎ ﺍﻧﺘﻘﺎﻝ ﺑﻪ ﻫﻢ ﺗﺒﺪﯾﻞ ﺷﻮﻧﺪ، ﯾﮑﺴﺎﻥ ﻣﺤﺴﻮﺏ ﻣﯽﺷﻮﻧﺪ. ﺣﺎﻻ ﺷﻤﺎ ﺑﺮﺍﯼ ﻭﺣﯿﺪ ﮐﺎﺷﯽﮐﺎﺭ، ﯾﮏ ﺑﺮﻧﺎﻣﻪ ﺑﻨﻮﯾﺴﯿﺪ ﮐﻪ ﺗﻌﺪﺍﺩ ﺍﺷﮑﺎﻝ ﻣﺨﺘﻠﻔﯽ ﮐﻪ ﻭﺣﯿﺪ ﻣﯽﺗﻮﺍﻧﺪ ﺑﺴﺎﺯﺩ ﺭﺍ ﺑﺸﻤﺎﺭﺩ.

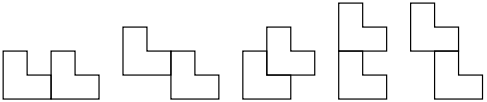
ﺑﺮﺍﯼ ﻣﺜﺎﻝ ﺍﮔﺮ ﺑﻪ ﻭﺣﯿﺪ ۲ ﺗﺎ ﺍﺯ کاشی ﺭﻭﺑﺮﻭ ﺑﺪﻫﯿﻢ ﻭ ﺑﻪ ﺍﻭ ﺑﮕﻮﯾﯿﻢ ﺍﯾﻦ ﮐﺎﺷﯽﻫﺎ ﺭﺍ ﺩﺭ یک جدول $10 \times 10$ بچین، ﺍﻭ ﺑﻪ ۵ ﻃﺮﯾﻖ ﺯﯾﺮ ﻣﯽﺗﻮﺍﻧﺪ ﺍﯾﻦﮐﺎﺭ ﺭﺍ ﺍﻧﺠﺎﻡﺩﻫﺪ.

ﺳﻄﺮ ﻧﺨﺴﺖ ﻭﺭﻭﺩﯼ ﺷﺎﻣﻞ ﺳﻪ ﻋﺪﺩ ﻃﺒﯿﻌﯽ ﺍﺳﺖ: $w،h$ و $k$. در سطر دوم $ h'$ و $ w'$ داده شده است. در $ h'$ سطر بعدی نیز در هر سطر $ w'$ عدد ۰ یا ۱ آمده است. این $h'$ سطر باطبع کاشی‌ای که به ﻭﺣ‰ﯿ‰ﺪ ﮐ‰ﺎﺷ‰ﯽﮐ‰ﺎﺭ ﺩﺍﺩﻩﺍﯾ‰ﻢ ﺭﺍ ﻣ‰ﺸ‰ﺨ‰ﺺ ﻣ‰ﯽﮐ‰ﻨ‰ﻨ‰ﺪ. ﺍﮔ‰ﺮ ﻣ‰ﻘ‰ﺪﺍﺭ ﺧ‰ﺎﻧ‰ﻪﺍﯼ ﺍﺯ ﺍﯾ‰ﻦ ﺟ‰ﺪﻭﻝ $h'\times w'$، ۱ باشد، ﯾ‰ﻌ‰ﻨ‰ﯽ ﺍﯾ‰ﻦ ﺧ‰ﺎﻧ‰ﻪ ﺟ‰ﺰﺀ ﮐ‰ﺎﺷ‰ﯽ ﺍﺳ‰ﺖ ﻭ ﻣ‰ﻘ‰ﺪﺍﺭ ﺻ‰ﻔ‰ﺮ ﺑ‰ﻪ ﻣ‰ﻌ‰ﻨ‰ﯽ ﺁﻥ ﺍﺳ‰ﺖ ﮐ‰ﻪ ﺍﯾ‰ﻦ ﺧ‰ﺎﻧ‰ﻪ ﺟ‰ﺰﺀ ﮐ‰ﺎﺷ‰ﯽ ﻧﯿﺴﺖ. ﺑﺪﯾﻬﯽ ﺍﺳﺖ ﺍﺯ ﺧﺎﻧﻪﻫﺎﯼ ﺻﻔﺮ ﺍﻃﺮﺍﻑ ﯾﮏ ﮐﺎﺷﯽ ﻣﯽﺗﻮﺍﻥ ﺻﺮﻑ ﻧﻈﺮ ﮐﺮﺩ.($1\leq k\leq 10$، $1\leq w' \leq w \leq 30$ و $1\leq h' \leq h \leq 30$)

ﺩﺭ ﺧﺮﻭﺟﯽ ﺑﺎﯾﺪ ﺗﻌﺪﺍﺩ ﺷﮑﻞﻫﺎﯼ ﻣﺘﻔﺎﻭﺗﯽ ﮐﻪ ﻭﺣﯿﺪ ﮐﺎﺷﯽﮐﺎﺭ ﻣﯽﺗﻮﺍﻧﺪ ﺑﺴﺎﺯﺩ ﺭﺍ ﺑﻨﻮﯾﺴﯿﺪ.

• محدودیت زمان: ۵ ثانیه
• محدودیت حافظه: ۲۵۶ مگابایت

• سوال بعد
• سوال قبل