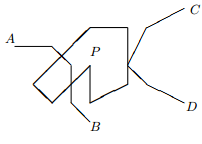
$n$ ضلعی ساده‌ی $P$ روی صفحه داده شده است. یک مسیر (خم یا خط شکسته) ﺑﯿﻦ ﺩﻭ ﻧﻘﻄﻪﯼ ﺩﻝﺧﻮﺍﻩ ﺭﻭﯼ ﺻﻔﺤﻪ ﺭﺍ«ﺧﻮﺏ» ﻣﯽﻧﺎﻣﯿﻢ ﺍﮔﺮ ﺑﺎ $P$ اشتراک داشته باشد (حتی در یک نقطه و با یکی از اضلاع). مثلا در شکل روبه‌رو مسیرهای $AB$ و $CD$ مسیرهایی خوب هستند.

دو نقطه‌ی $s$ و $t$ روی صفحه داده شده‌اند. می‌دانیم $s$ و $t$ داخل $P$ یا روی اضلاع آن نیستند. شما باید طول کوتاه‌ترین مسیر خوب از $s$ به $t$ را بیابید.

برنامه‌ای بنویسید که:

• مشخصات $P$ و $q$ جفت نقطه‌ی $s_i$ و $t_i$ را از ورودی بخواند.
• طول کوتاه‌ترین مسیر خوب بین هر $s_i$ و $t_i$ را پیدا کند و در خروجی بنویسد.

در سطر اول ورودی، دو عدد صحیح $n$ و $q$ به ترتیب نوشته شده‌اند.($1\leq n,q \leq 1000$)

در هر یک از $n$ سطر بعدی، دو عدد $x$ و $y$ نوشته شده است که مختصات یک راس از $P$ را مشخص می‌کند. رئوس $P$ به ترتیب ساعت‌گرد یا پادساعت‌گرد داده شده‌اند.

در سطر $i$ام از $q$ سطر بعدی، چهار عدد $x_1$، $y_1$، $x_2$ و $y_2$ نوشته شده‌اند که $(x_1,y_1)$ مختصات $s_i$ و $(x_2,y_2)$ مختصات $t_i$ است.

قدر مطلق تمام اعداد ورودی کم‌تر یا مساوی ۱۰۰۰ است و همه‌ی مختصه‌ها حداکثر تا ۴ رقم اعشار به شما داده می‌شوند.

در سطر $i$ام از خروجی طول کوتاه‌ترین مسیر خوب بین $s_i$ و $t_i$ را تا ۴ رقم اعشار بنویسید. عدد خود را به نزدیک‌ترین ضریب صحیح $10^{-4}$ گرد کنید.

• محدودیت زمان: ۵ ثانیه
• محدودیت حافظه: ۳۲ مگابایت

• سوال بعد
• سوال قبل