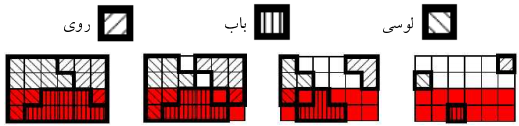
سه کودک قصد دارند که با استفاده از قطعات مربع شکل، پرچم لهستان را بسازند. این پرچم مستطیلی است به عرض $3n$ خانه و به ارتفاع $2n$ خانه؛ در این‌جا $n$ یک عدد صحیح مثبت است. به علاوه پرچم مذکور شامل $3n^2$ مربع سفید و $3n^2$ مربع قرمز است. کودکان این قطعات را ر روی یک میز مستطیلی شکل قرار می‌دهند. بر روی این میز برای $6n^2$ قطعه جا وجود دارد؛ قطعات سفید باید در $n$ سطر بالایی و قطعات قرمز در $n$ سطر پایینی قرار بگیرند. سطرها از بالا به پایین، با شماره‌های ۱ تا $2n$ نام‌گذاری شده‌اند و ستون‌ها نیز از چپ به راست با شماره‌های ۱ تا $3n$.

کودکان به نوبت قطعات را بر روی میز قرار می‌دهند. در حرکت اول، لوسی قطعه‌ی خود را در محل $(1,l)$ در ضلع سمت چپ می‌گذارد؛ باب قطعه‌ی خود را در محل $(3n,r)$ بر ضلع سمت راست می‌گذارد. می‌دانیم که $1\leq l ، r<2n$ و $1<b<3n$ است.

در هر یک از نوبت‌های بعدی به این شکل بازی می‌کنند: هر کودک می‌تواند در محلی قطعه‌اش را قرار دهد که اولا خالی باشد و ثانیا آن محل مجاور محلی باشد که در نوبت پیش در آن قطعه‌ای گذارده است؛ دو خانه مجاورند اگر ضلع مشترکی داشته باشند. در هر نوبت، هر کودکی تا حد امکان قطعاتش را بر روی میز قرار می‌دهد. در هر خانه حداکثر می‌توان یک قطعه را جای داد؛ لذا اگر چند کودک در یک نوبت قصد قرار دادن قطعه‌هایشان را در یک خانه داشته باشند، اولویت به ترتیب با لوسی، باب و در نهابت روی می‌باشد.

پیش از شروع بازی، کودکان باید قطعه‌ها را بین خود تقسیم کنند. مسئله این‌جاست که آن‌ها نمی‌دانند هر کدام چند قطعه از هر رنگ نیاز دارند. به کودکان کمک کنید و تعداد قطعاتی که هر یک نیاز دارند را محاسبه کنید.

برنامه‌ای بنویسید که:

• اندازه‌ی میز، یعنی $n$ و جای قطعات اولیه، یعنی $b،l$ و $r$ را از ورودی بخواند.
• تعداد قطعات از هر رنگ که هر یک لازم دارند را حساب کند.
• پاسخ را در خروجی بنویسید.

سطر نخست ورودی شامل چهار عدد صحیح است: $b،l،n$ و $r$ که با فاصله از هم جدا شده‌اند. می‌دانیم که $1\leq n \leq 10^9$، $r<2n$، $1\leq l$ و $1<b<3n$ می‌باشد. به اضافه در نیمی از موارد $n\leq 100$ خواهد بود.

در تنها سطر خروجی شش عدد صحیح باید بنویسید. اولین و دومین عدد، به ترتیب تعداد قطعات سفید و قرمزی است که لوسی نیاز خواهد داشت؛ عدد سوم و چهارم، به ترتیب تعداد قطعات سفید و قرمز مورد نیاز باب و عدد پنجم و ششم این مقادیر برای روی است.

• محدودیت زمان: ۲ ثانیه
• محدودیت حافظه: ۶۴ مگابایت

• سوال بعد
• سوال قبل