فهرست مندرجات
بالتازار و سفر به فرانسه
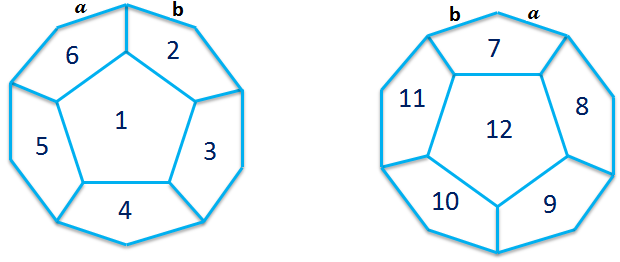
پروفسور بالتازار پروپا قرص فوتبال است. چند روز پیش از تولدش قصد رفتن به جام جهانی ۹۸ را داشت که دوستش سر رسید و به او هدیه‌ای داد. هدیه یک ۱۲ وجهی است که تمامی وجه‌هایش ۵ ضلعی‌های برابر هستند. هر یک از وجوه با یک عدد بین ۱ تا ۱۲ مشخص شده‌اند و در شکل زیر می‌توانید شکل کلی این هدیه را ببینید.
توجه کنید که این دو نصفه‌ی شکل به هم چسبیده‌اند، طوری که وجه‌های همسایه‌ی ۷ وجوه ۲، ۱۱، ۱۲، ۸ و ۶ هستند و در واقع دو نصفه از روی یال‌های $a$ و $b$ به‌هم چسبیده‌اند.
این هدیه در واقع یک پازل است که دوست بالتازار برایش خریده تا در حال دیدن مسابقه بتواند با آن بازی کند. به جز این ۱۲ وجهی، ۱۲ کاشی ۵ ضلعی دیگر هم هست که روی ضلع‌هایشان اعدادی از بین ۰، ۱ و ۲ نوشته شده و هر کاشی روی یکی از وجه‌های ۱۲ وجهی می‌تواند به ۵ روش مختلف قرار گیرد.
حال می‌خواهیم طوری این کاشی‌ها را روی ۱۲ وجهی قرار دهیم که اضلاع مشترکشان هم عدد باشند.
ورودی
فایل ورودی دارای ۱۲ سطراست که برای هر $i$ $(1\leq i \leq 12)$، سطر $i$ ام ۵ عدد از بین ۰، ۱ و ۲ دارد که ضلع‌های یک کاشی را به ترتیب ساعت‌گرد نشان می‌دهد. ضلعی که توضیحات یک کاشی با آن شروع می‌شود را ضلع مقیاس آن کاشی می‌گوییم.
خروجی
فایل خروجی نیز ۱۲ خط دارد و در آن مشخصات یک پازل حل شده قرار گرفته است. در سطر $i$، ۲ عدد $t$ و $n$ آمده است که می‌گوید کاشی $t$ بر وجه با عدد $i$ قرار گرفته است. $n$ مشخص می‌کند که کاشی دقیقا چطور روی وجه ۱۲ ضلعی قرار گرفته است. در واقع $n$ عدد وجه همسایه‌ی ضلع مقیاس کاشی $t$ ام است.
اگر راه حلی برای پازل وجود ندارد در فایل خروجی تنها یک ۱- چاپ کنید.
ورودي و خروجي نمونه
| ورودي نمونه | خروجي نمونه |
|---|---|
| 0 0 1 1 2 0 2 1 0 1 2 0 1 0 1 0 0 1 2 1 0 2 1 1 2 2 0 1 2 1 0 2 1 2 1 2 2 1 0 1 1 2 2 0 0 0 2 1 0 2 0 2 1 2 0 2 0 1 2 0 | 1 2 3 7 12 4 7 9 9 1 11 8 8 2 4 6 5 4 2 12 6 3 10 7 |
| 1 0 2 0 2 2 2 2 1 2 1 1 0 0 0 1 1 0 2 1 2 1 1 1 1 1 2 2 1 1 2 1 2 2 1 2 2 0 1 0 0 1 2 1 2 2 2 1 0 0 1 2 0 2 0 2 2 2 0 1 | 1 2 2 7 8 2 7 1 11 4 12 2 5 2 3 12 10 5 9 3 6 10 4 7 |
ابزار صفحه
کلیه‌ی حقوق این سایت متعلق به کمیته‌ی ملی المپیاد کامپیوتر ایران است.
