هر عدد طبیعی مانند $n$ را می‌توان به صورت $n=d_1\times 1!+d_2\times 2!+...+d_k\times k!$ نمایش داد که در آن $k$ و $d_i$ ها اعداد صحیح نامنفی هستند و $d_i\leq i$ است. به این عمل نمایش عدد $n$ در مبنای فاکتوریل می‌گوییم. برای مثال عدد $83_10$ را می‌توان به صورت $31210_!$ در مبنای فاکتوریل تعریف کرد. زیرا $3 * 4! + 1 * 3! + 2 * 2! + 1 * 1! + 0 * 0! = 83$.

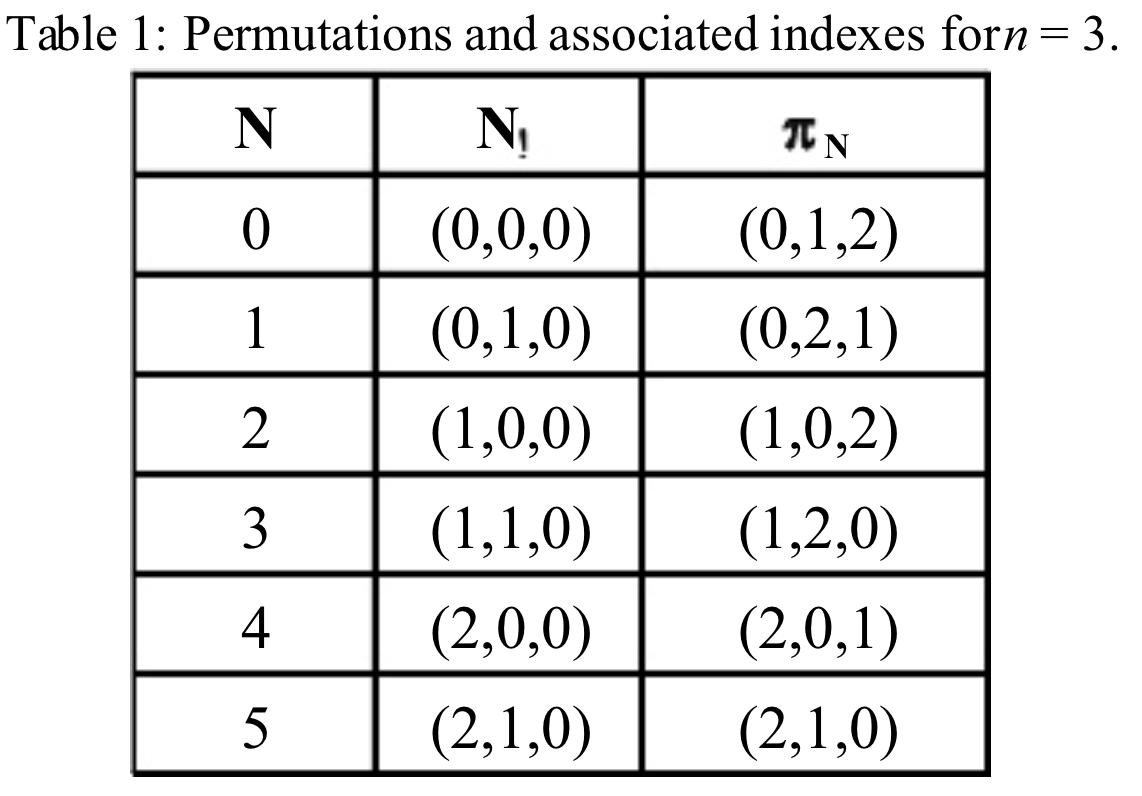
به ازای $n$ یک جایگشت مانند $p$ را به صورت $p_0, p_1, ... , p_n$ تعریف می‌کنیم. برای مثال به ازای $n = 5$ اگر جایگشت‌ها را به ترتیب الفبایی بنویسیم، $\pi_0 = (0, 1, 2, 3, 4)$ و $\pi_{83} = (3, 1, 4, 2, 0)$. به ازای هر اندیس $i$ تعداد خانه‌هایی مانند $j$ که $j > i$ و $\pi_i > \pi_j$ را $l_i(\pi)$ می‌نامیم که همان تعداد نابجایی‌های اندیس $i$ است. بردار $L$ را به صورت زیر تعریف می‌کنیم:

$L(\pi) = (l_0(\pi), l_1(\pi), ... l_{n - 1}(\pi))$

به سادگی اثبات می‌شود که این کد هر جایگشت یک کد یکتا دارد. این کد را کد لمر یا lehmer code می‌نامیم. حال به ازای جایگشت $\pi_{83}$ می‌بینیم که کد لمر آن برابر با $(3, 1, 2, 1, 0)$ است. بدین ترتیب هر عدد در مبنای فاکتوریل را به کمک کد لهمر می‌توانیم به یک جایشگت یکتا متناظر کنیم.

در بخش قبل تقریبا نشان دادیم چگونه از یک جایگشت عدد متناظر آن را بسازیم. مراحل آن به شرح زیر است:

• ابتدا با محاسبه‌ی بردار نابجایی‌های آن کد لمر آن را بدست می‌آوریم.
• سپس کد لمر را که همان نمایش عدد در مبنای فاکتوریل است به عدد تبدیل می‌کنیم.

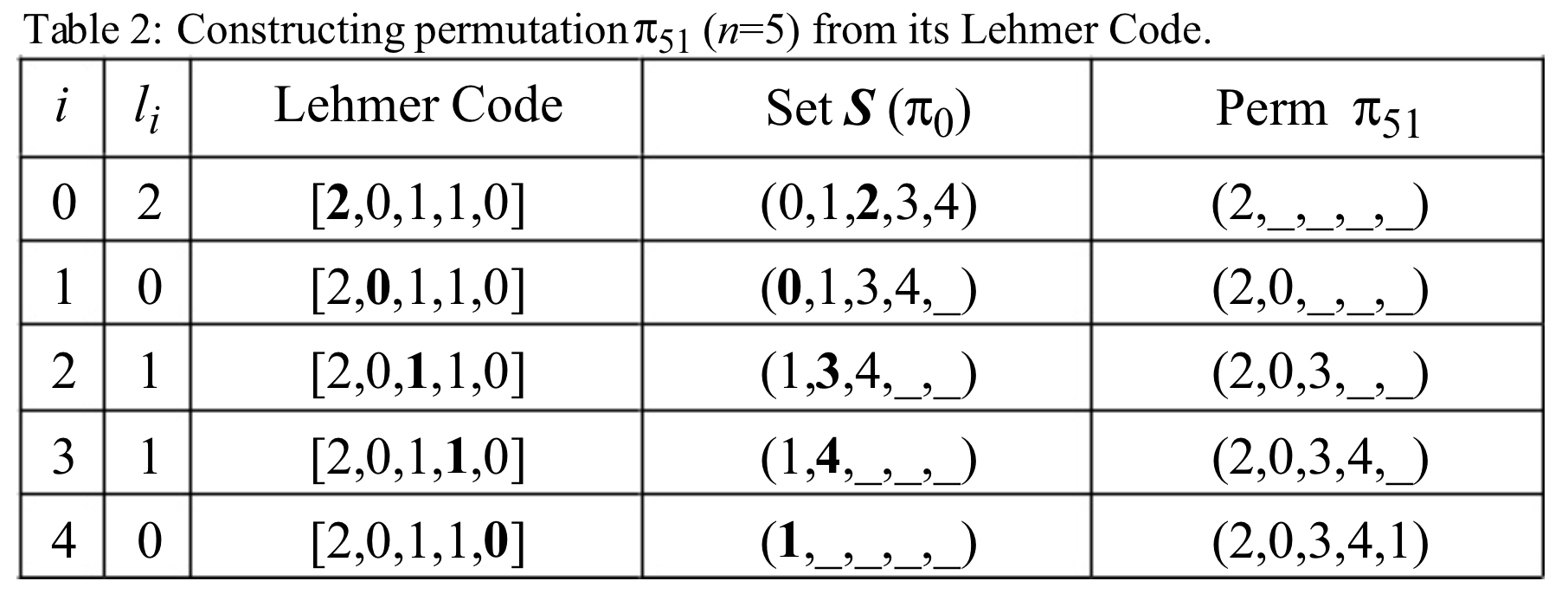
در مرحله‌ی اول عدد را در مبنای فاکتوریل می‌نویسیم و کد لمر آن را بدست می‌آوریم. اولین عدد کد لمر نشان‌دهنده‌ی اولین عدد جایشگت است زیرا همه‌ی اعداد در اندیس‌های بعدی آمده‌اند و تعداد نابجایی‌هایی که می‌سازد برابر با مقدار خودش است. با همین روند می‌توان دریافت که با الگوریتم زیر می‌توان جایشگت را از کد لمر ساخت:

• مجموعه‌ی $S$ را برابر با جایشگت مرتب یعنی $(0, 1, ... , n)$ قرار می‌دهیم.
• به ازای $i$ از $0$ تا $n - 1$ کار زیر را انجام می‌دهیم:
  • مقدار $\pi_i$ را برابر با $S(l_i(\pi))$ قرار می‌دهیم.
  • عضو $l_i(\pi)$ام را از مجموعه‌ی $S$ حذف می‌کنیم.

برای مثال ساخت جایگشت برای عدد $53$ را در شکل زیر می‌توان دید: