سوال ۳۸
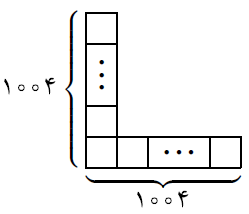
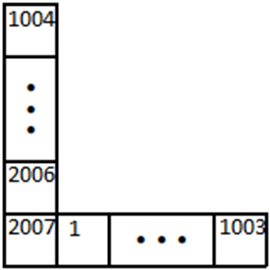
دوهزار و هفت عدد را در ۲۰۰۷ خانهی شکل روبهرو قرار دادهایم. در هر حرکت میتوان ۱۰۰۷ عدد موجود در هر ستون را از بالا به پایین و یا ۱۰۰۷ عدد موجود در سطر را از چپ به راست، به صورت صعودی مرتّب کرد. به یک جدول «پایدار» میگوییم اگر وضعیت آن جدول در صورت انجام هیچیک از این مرتبسازیها تغییر نکند. حدّاقل تعداد حرکاتی که میتوان با آنها هر جدولی را پایدار کرد چقدر است؟
- ۱۰۰۵
- ۱۰۰۷
- ۲۰۰۶
- ۳۰۰۹
- ۲۰۰۷
پاسخ
گزینهی (۵) درست است.
ثابت میکنیم حداکثر تعداد حرکات لازم ۲۰۰۷ تاست. میتوانیم هر جدول را با ۲۰۰۷ حرکت طوری مرتب کنیم که به ترتیب در خانههای ۱ تا ۲۰۰۷ قرار بگیرند.
در هر مرحله کمترین عضوی(کمتر از ۱۰۰۴)که در جای خود نباشد را پیدا کرده و با حداکثر ۲ حرکت در جای خود قرار میدهیم (اگر این عدد در ستون بود با یک بار مرتبسازی ستون و اگر در سطر بود ابتدا سطر را مرتب کرده چون کوچکترین عدد است به ابتدای سطر میآید سپس ستون را مرتب میکنیم.).
پس ستون جدول را با ۲۰۰۶ حرکت پر میکنیم، سپس با یک حرکت سطر جدول را که شامل ۱۰۰۴ عدد بزرگتر است مرتب میکنیم.
حال مثالی ارائه میدهیم که دقیقن ۲۰۰۷ حرکت لازم داشته باشد.
در این جدول حرکات یکتا هستند (دو حرکت مشابه پشت هم بیهوده است از طرفی اولین حرکت باید روی سطر باشد) در هر ۲ حرکت دقیقا یک عدد در ستون سر جای خود قرار میگیرد.