سوال ۱۲
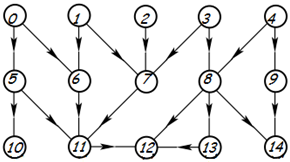
در شکل روبهرو ۱۵ دفتر اداریِ یک سازمان نشان داده شده است. هر دفتر، تعدادی دفتر زیر دست دارد. این ارتباط در شکل با پیکانهایی از دفترها به دفترهای زیردستشان نمایش داده شده است. هر دفتر، بدین صورت عمل میکند: هر نامهای را که دریافت میکند برای هرکدام از دفترهای زیردستش کپی میکند و میفرستد (دفترهای زیردست هم همین کار را انجام میدهند). دفترهای ردیف بالا از چپ به راست به ترتیب شمارههای ۰ تا ۴ را دارند. طی ۲۰۰۷ روز، این دفترها به این صورت کار کردهاند که در روز iاُم (۱≤i≤۲۰۰۷) از بیرون سازمان به دفتر kاُمِ ردیف بالا (۰≤k≤۴)٬ i+k نامه میرسد.
اگر پس از انجام همهی این عملیّات اداری طی این ۲۰۰۷ روز، مجموع تعداد نامههای دریافت شده توسط ادارههای سطر پایین، n باشد، باقیماندهی تقسیم عدد n بر ۵ کدام است؟
- ۰
- ۱
- ۲
- ۳
- ۴
پاسخ
گزینهی (۴) درست است.
در بالا 15 دفتر را به صورت شمارهگذاری شده مشاهده میکنید. برای اینکه محاسبه کنیم در نهایت به هرکدام از دفاتر 10 تا 14 چند نامه میرسد کافی است که تعداد نامههای آنها را بر حسب تعداد نامههای دفاتر 0 تا 4 محاسبه کنیم.
10=0
11=0+(0+1)+(1+2+3)
12=(0+(0+1)+(1+2+3))+(3+4)+((3+4))
13=(3+4)
14=(3+4)+4
جمع کل = 0×5+1×4+2×2+3×6+4×5
به دفتر kام در کل به مقدار زیر نامه خواهد رسید:
K×2007+2007×20082=2×k+3(mod5)
در نتیجه در کل جمع کل به پیمانه 5 برابر با 3 خواهد بود و گزینه د صحیح است.