سوال ۳۹
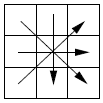 یک جدول ۳×۳ از اعداد ۱ تا ۵ موجود است. اگر ارقام موجود در هر یک از سطرها را از چپ به راست٬ ارقام هر یک از ستونها را از بالا به پایین٬ و نیز ارقام دو قطر را به صورت شکل مقابل کنار هم بنویسیم٬ ۸ عدد سه رقمی به دست خواهد آمد. اگر ٬۱۱۲ ٬۱۲۱ ٬۱۲۳ ٬۱۵۳ ٬۲۴۳ ٬۳۱۳و ٬۳۲۲ ۷تا از این اعداد باشند٬ عدد هشتم کدام است؟
یک جدول ۳×۳ از اعداد ۱ تا ۵ موجود است. اگر ارقام موجود در هر یک از سطرها را از چپ به راست٬ ارقام هر یک از ستونها را از بالا به پایین٬ و نیز ارقام دو قطر را به صورت شکل مقابل کنار هم بنویسیم٬ ۸ عدد سه رقمی به دست خواهد آمد. اگر ٬۱۱۲ ٬۱۲۱ ٬۱۲۳ ٬۱۵۳ ٬۲۴۳ ٬۳۱۳و ٬۳۲۲ ۷تا از این اعداد باشند٬ عدد هشتم کدام است؟
- ۵۲۴
- ۴۲۵
- ۲۵۴
- ۵۱۴
- ۴۱۵
پاسخ
معلوم است که عدد موجود در خانه وسط٬ چهار بار به عنوان رقم وسط یک عدد سه رقمی ظاهر میشود ولی در بین اعداد داده شده هیچ چهار عددی وجود ندارد که رقم وسط مشابهی داشته باشند٬ ولی سه عدد ۱۲۳٬۱۲۱ و ۳۲۲ چنانند که رقم وسطشان ۲ است٬ بنابراین عدد مجهول نیز رقم وسطش ۲ است که در بین گزینهها فقط ۱ و ۲ چنینند. عدد a به عنوان رقم اول در ۳ تا از اعداد ظاهر میشود که در بین ۸ عدد فقط رقم ۱ در بیش از دو عدد بهعنوان رقم اول ظاهر شده است٬ بنابراین a=1. قطر اصلی به صورت 12i میباشد که اگر i را برابر ۱ 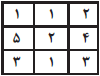 قرار دهیم آنگاه ستون سوم به صورت cf1 در میآید که در بین ۸ عدد چنین چیزی وجود ندارد٬ بنابراین i=3 و حرف g به عنوان رقم صدگان دو عدد به کار میرود که یکی از آن دو رقم یکانش ۳ است و دیگری رقم دهگانش ۲ است٬ در بین ۸ عدد فقط دو عدد ۳۱۳ و ۳۲۲ چنینند. لزا g=3،h=1 و c=2. بعد از این جدول به صورت منحصربهفرد به شکل مقابل پر میشود که در آن عدد مجهول عدد موجود در سطر دوم به شکل ۵۲۴ یافت میشود.
قرار دهیم آنگاه ستون سوم به صورت cf1 در میآید که در بین ۸ عدد چنین چیزی وجود ندارد٬ بنابراین i=3 و حرف g به عنوان رقم صدگان دو عدد به کار میرود که یکی از آن دو رقم یکانش ۳ است و دیگری رقم دهگانش ۲ است٬ در بین ۸ عدد فقط دو عدد ۳۱۳ و ۳۲۲ چنینند. لزا g=3،h=1 و c=2. بعد از این جدول به صورت منحصربهفرد به شکل مقابل پر میشود که در آن عدد مجهول عدد موجود در سطر دوم به شکل ۵۲۴ یافت میشود.
