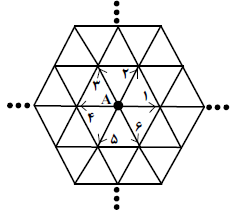
سوال ۲۶

گزینه (۱) درست است.

برای آن‌که شخص پس از ۴ حرکت به نقطه‌ی $A$ برگردد باید یکی از سه حالت زیر اتفاق بیفتد:

1. شخص روی یک لوزی حرکت کند. احتمال آن‌که حرکت اول٬ دوم٬ سوم و چهارم شخص مطلوب باشد به ترتیب $\frac{1}{6}،\frac{4}{6}،\frac{6}{6}$ و $\frac{1}{6}$ می‌باشد که دراین صورت احتمال رسیدن به مقصد با طی کردن یک لوزی برابر $\frac{1}{6} \times \frac{4}{6} \times \frac{6}{6} \times \frac{1}{6}$؛ یعنی $\frac{4}{216}$ خواهد بود.
2. شخص یک پاره‌خط به طول ۲(نه لزوما پاره‌خط راست) را طی کرده و همان مسیر را برگردد که دراین صورت احتمال مطلوب بودن حرکات اول٬دوم٬سوم و چهارم به ترتیب برابر $\frac{1}{6}،\frac{5}{6}،\frac{6}{6}$ و $\frac{1}{6}$ خواهد بود.بنابراین احتمال رسیدن به مقصد به طریق اشاره شده برابر $\frac{1}{6} \times \frac{5}{6} \times \frac{6}{6} \times \frac{1}{6}$؛ یعنی $\frac{5}{216}$ خواهد بود.
3. ابتدا شخص یکی از ۶ پاره‌خط اطراف خود را به صورت رفت و برگشت طی کرده و سپس همین عمل را با همان پاره خط دیگر تکرار می‌کند٬ که در این صورت احتمال مطلوب بودن هر یک از حرکات چهارگانه او به ترتیب $\frac{6}{6}،\frac{1}{6}،\frac{6}{6}$ و $\frac{1}{6}$ و در کل $\frac{6}{216}$ می‌باشد.

با در نظر گرفتن سه حالت ممکن احتمال رسیدن به مقصد $\frac{6}{216}+\frac{5}{216}+\frac{4}{216}$؛ یعنی ‎$5\over 72$ می‌باشد.