سوال ۲۰
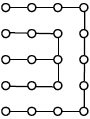امید و حمید با هم نقطه‌بازی می‌کنند. قاعده‌ی بازی به این صورت است که هر نفر در نوبت خود باید یک نقطه را به یک نقطه‌ی مجاور آن که قبلاً به آن وصل نشده، متصل کند و هرگاه یک نفر یک مربع $1 \times 1$ را کامل کرد، باید یک حرکت دیگر به‌عنوان جایزه انجام دهد (دو نقطه در صورتی مجاورند که فاصله‌ی آن‌ها یک باشد). امتیاز یک فرد در انتهای بازی برابر تعداد مربع‌های $1 \times 1$ است که او کامل کرده است. نوبت حمید است که بازی کند و وضعیت بازی به شکل روبه‌رو است. در نهایت اگر هر نفر بهترین بازی خود را انجام دهد، بازی با چه نتیجه‌ای تمام می‌شود؟
- ۱۰ بر ۲ به نفع امید
- ۸ بر ۴ به نفع امید
- ۴ بر ۸ به نفع حمید
- ۳ بر ۹ به نفع حمید
- ۲ بر ۱۰ به نفع حمید
پاسخ
گزینه (۵) درست است.
ابتدا حمید پاره‌خط‌های $AB،EF$ و $BC$ را کشیده و دو امتیاز کسب می‌کند٬ سپس امید پاره‌خط‌های $FG$ را کشیده و دو امتیاز کسب می‌کند و جایزه‌ی خود را یکی از پاره‌خط‌های باقی‌مانده انتخاب کرده و رسم می‌کند. این پاره‌خط هر پاره‌خطی(مانند $CD$) می‌تواند باشد٬ همه‌ی امتیازات باقی‌مانده که ۸ امتیاز می‌باشد را نصیب حمید خواهد کرد.