فهرست مندرجات
Pull the String
یک میز چوبی داریم که $n$ میخ باریک تا نیمه بر روی سطح آن کوبیده شدهاند. برای مشخص کردن نقاط روی سطح میز از مختصات $(x,y)$ آنها استفاده میکنیم. یک نخ نازک هم به شکل خط شکستهای روی سطح میز قرار گرفته است، به طوری که در طول مسیرش $x$ آن افزایش مییابد. به عبارتی دیگر برای تمام نقاط آن میتوان با داشتن مختصهی $x$ به طور یکتا مختصهی $y$ نخ را در صورت وجود تعیین کرد. دو سر نخ از درون دو سوراخ ریز به زیر میز رفتهاند. اگر دو سر نخ را از زیر میز بکشیم، طول نخ روی میز تا اندازهای کاهش مییابد که از روی میخی عبور نکرده باشد. به عنوان مثال اگر در وضعیت اولیه، نخ از بالای یک میخ عبور کرده باشد(با مختصهی $y$ بیشتر)، کشیدن آن نمیتواند باعث شود که در وضعیت پایانی، نخ از پایین همان میخ عبور کند. واضح است که اگر نخ را کاملا بکشیم، وضعیت نهایی طوری خواهد بود که طول نخ در بین حالتهای مجاز (بدون عبور از میخها)، کمینه باشد. میخواهیم شکل نخ را در وضعیت نهایی(پس از کشیدن آن تا جای ممکن) محاسبه کنیم.
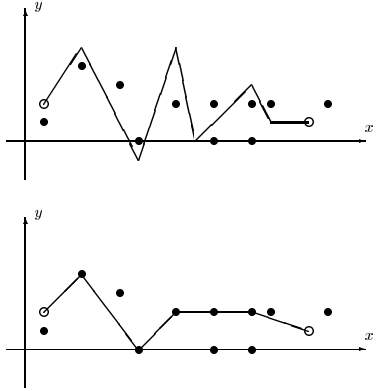
به عنوان مثال، در شکل زیر میخها با دایرههای سیاه و سوراخها با دایرههای سفید نشان داده شدهاند. شکل بالایی نشاندهندهی وضعیت اولیهی نخ است و شکل پایین وضعیت نهایی نخ را پس از کشیده شدن نمایش میدهد.
برنامهای بنویسید که:
- مکان میخها و وضعیت اولیهی نخ را از ورودی بخواند.
- شکل نخ را پس از کشیده شدن دو سرش از سوراخها محاسبه کند.
- شکل نهایی نخ را پس از کشیده شدن در خروجی بنویسید.
ورودی
- در سطر اول ورودی، عدد $n$(تعداد میخها) قرار دارد. در هر یک از $n$ سطر بعد، دو عدد صحیح $x$ و $y$ با یک فاصله از هم آمدهاند که مختصات $(x,y)$ را برای یک میخ نشان میدهند. مختصات هیچ دو میخی یکسان نمیباشد.
- در سطر بعد (سطر $(n+2)$ام)، عدد $m$ نوشته شده است که نشان میدهد نخ در وضعیت اولیه، صرف نظر از دو سرش، ($m-2$) نقطهی شکستگی دارد. در هر یک از $m$ سطر بعد، دو عدد صحیح $x$ و $y$ با یک فاصله از هم آمدهاند که مختصات $(x,y)$ را برای یک نقطهی شکستگی (یا سوراخ) نشان میدهند. این نقاط از سوراخ چپ (با $x$ کمتر) شروع میشوند و به ترتیب از چپ به راست ادامه مییابند و با سوراخ راست (با $x$ بیشتر) پایان مییابند. پس نقاط بر حسب مختصهی $x$ از کوچک به بزرگ مرتب شدهاند. هیچ سه نقطهی متوالی از این نقاط در یک خط نیستند.($2\leq m \leq 10^5$ و $0\leq n \leq 10^5$)
- در ابتدای کار نخ با هیچ یک از میخها تماس ندارد یا به عبارتی دیگر از روی هیچ میخی رد نشده است. همچینین هیچ میخی روی سوراخها قرار ندارد.
- مختصههای نقاط ورودی همگی اعداد صحیحاند و قدر مطلق هیچ کدامشان از $10^9$ بیشتر نمیشود. در ضمن از قطر نخ، میخها و سوراخها صرف نظر کنید.
خروجی
- در سطر اول خروجی، عدد $k$ را بنویسید که نشان میدهد نخ در وضعیت نهایی (پس از کشیده شدن) صرف نظر از دو سرش، $k-2$ نقطهی شکستگی دارد.
- در $k$ سطر بعد، مختصات دو سوراخ و نقاط شکستگی نخ پس از کشیده شدن را مشابه وضعیت اولیهی نخ در ورودی (از چپ به راست) بنویسد. دقت کنید که نخ باید در نقاط شکستگی حتما شکسته شده باشد، یعنی هیچ سه نقطهی متوالی در خروجی نباید در یک خط راست باشند.
محدودیتها
- محدودیت زمان: ۲ ثانیه
- محدودیت حافظه: ۴۰ مگابایت