فهرست مندرجات
درخت های ریشه دار
در نظریهٔ گراف، یک «درخت ریشهدار» (Rooted Tree) به درختی گفته میشود که یک رأس در آن به عنوان ریشه برچسب خورده باشد. درخت ریشهدار یک ساختار داده کلیدی در علوم کامپیوتر است.
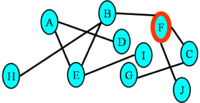
رأسهایی که به طور مستقیم به رأس دیگری متصل اند بچههای آن نامیده میشوند. مثلاً در شکل روبرو $E$ و $H$ بچههای $B$ هستند و $B$ پدر آنهاست. همچنین اگر یک رأس بچهای نداشته باشند به آن برگ میگویند.(مانند گره $G$)
تعداد درختهای ریشه دار با $n$ رأس بر اساس دنباله روبرو است: ۱, ۱, ۲, ۴, ۹, ۲۰, ۴۸, ۱۱۵, ۲۸۶, ۷۱۹, ۱۸۴۲, ۴۷۶۶,… (http://mathworld.wolfram.com/RootedTree.html Rooted Tree, Wolfram MathWorld)
درخت $m$-تایی پر: درختی که هر راس داخلی آن دقیقا $m$ فرزند دارد.
- درخت $m$-تایی پر که دارای $n$-تا راس ، $i$-تا راس داخلی و $l$-تا برگ باشد ، روابط زیر برقرار است:
*
- $mi+1$ = $n$
- ($m-1$)/($ml-1$) = $n$
- $m$/($n-1$) = $i$
- ($m-1$)/($l-1$) = $i$
- $m$/[$1$+$n$($m-1$)] = $l$
- $1$+$i$($m-1$) = $l$
درخت $m$-تایی متقارن : درختی است که زیر درخت های ریشه ی آن دارای مسیر های تقریبا هم اندازه باشد. (اختلاف مسیر ها در حد $1$ یا $2$ باشد.)
سطح هر راس($Level$) : به طول کوتاه ترین مسیر از ریشه تا راس مورد نظر را سطح ($Level$) آن راس می گویند.
ارتفاع درخت($Height$): به ماکزیمم سطح هر درخت ارتفاع ($Height$)آن می گویند.
-اگر در درخت $m$-تایی ، $m$ را به توان ارتفاع برسانیم ، حداکثر تعداد برگ ها بدست می آید.
درخت دودویی
تعریف
در علوم رایانه، یک «درخت دودویی» یک ساختمان داده ی درخت است که در آن هر گره حداکثر دو گره فرزند دارد که فرزندان راست و چپ نامیده میشوند.درختهای دودویی برای پیادهسازی«درخت جستجوی دودویی» و «انبوه دودویی» و برای جستجوی کارآمد و مرتبسازی استفاده میشود. درخت دودویی یک حالت خاص از یک «درخت $k$-تای» است ،که در آن $k$ برابر $2$ میباشد.
انواع درختان دودویی
- «درخت دودویی ریشهدار» یک درخت با یک گره ریشه است که در آن هر گره حداکثر دو فرزند دارد.
- «درخت دودویی پر»(گاهی اوقات «درخت دودویی مناسب» یا «$2$_ درخت» یا «درخت اکیداً دودویی» گفته میشود ) یک درخت که در آن هر گره به غیر از برگها دارای دو فرزند است.هر گره در درخت دودویی دارای دو فرزند یا بدون فرزند است .یک درخت پر گاهیاوقات بهطور ابهامانگیزی به عنوان «درخت دودویی کامل» تعریف میشود.فیزیکدانان یک «درخت دودویی» را بهعنوان «درخت دودویی پر» تعریف میکنند.
- «درخت دودویی کامل» ($complete$) یک درخت دودویی است که در آن هر سطح ،به جز احتمالاً آخرین سطح،بهطور کامل پر شدهاست، و همۀ گرهها تا جایی که ممکن است در چپ درخت قرار میگیرند.درختی که این استثنا را داشتهباشد که سطح آخر آن کاملاً پر نباشد، درخت دودویی تقریباً کامل یا نزدیک به درخت دودویی کامل گویند.این نوع درختان از ساختمان دادۀ ویژهای به نام «هیپ» استفاده میکنند.
- «درخت دودویی کامل نا محدود» درختی است که دارای بینهایت سطح قابلشمارش میباشد، که در آن هر گره دارای دو فرزند است بهطوریکه گرههای 2d در سطح $d$ هستند.مجموعۀ گرهها شمارای نامتناهی است ، ولی مجموعهای از بینهایت مسیر از ریشه ، ناشمارا است،که دارای «عدد کاردینالیتی پیوسته» است.این مسیرها رابطۀ دوسویی را با نقاط «مجموعۀ کانتر» ، یا مجموعهای از اعداد گنگ حفظ میکند.
- «درختی دودویی متوازن» که معمولاً بهعنوان درخت دودویی است که در آن اختلاف عمق زیردرخت چپ و راست آن $1$ یا کمتر است، اگر چه به طور کلی درخت دودویی است که هیچ برگی نسبت با برگهای دیگر فاصلۀ زیادی تا ریشه ندارد.(طرح توازن متمایز اجازه میدهد که تعریف متفاوتی از «بسیار دورتر» ارائه شود.) درخت دودویی هنگامی متوازن است که مطابق تعریف عمق آن قابل پیش بینی باشد.(بسیاری از گرهها از ریشه تا برگ پیموده میشوند ، چنانکه شمارۀ ریشه به عنوان گرۀ $0$ و بقیۀ گرهها اعداد n … 2 1 را میگیرند.) این عمق (ارتفاع هم نامیده میشود) برابر قسمت صحیح (
log2(n است، که در آن $n$ تعداد گرهها در درخت متوازن است. مثلاً، برای درخت متوازنی که دارای $1$ گره است ، log2(1)=0 ،درنتیجه عمق درخت برابر صفر است.برای یک درخت متوازن با $100$ گره ، log2(100)=6.64 ،درنتیجه عمق درخت برابر $6$ است. - - » درخت منحط» درختی است که هر گرۀ والدین فقط به یک گرۀ فرزند متصل است.این به این معنی است که عملکرد این درخت مانند رفتار ساختمان دادۀ «لیست پیوندی» است.
خواص درخت دودویی
- تعداد $n$ گره در «درخت دودویی کامل» را میتوان با استفاده از این فرمول بدست آورد :n
= 2که در آن $h$ ارتفاع درخت است.h+ 1 - 1
- تعداد $n$ گره در درخت دودویی با ارتفاع $h$ حداقل برابر n = h + 1 و حداکثر n
= 2است.h+ 1 - 1
- تعداد $n$ گره در «درخت دودویی کامل» را همچنین میتوان با استفاده از این فرمول بدست آورد : n
= 2 l - 1که در آن $l$ تعداد برگهای درخت است.
- تعداد پیوندهای تهی (گرههای فرزند وجود ندارند) در «درخت دودویی کامل» با $n$ گره برابر (n
+ 1) است.
- تعداد گرههای داخلی (گرههای غیر از برگ یا n - l ) در درخت دودویی کامل با $n$ گره برابر (floor (n/2 است.
عملیات متداول
انواع عملیاتهای مختلف را میتوان روی درخت دودویی انجامداد.بعضی از عملیاتها تغیری ایجاد میکنند، درحالی که دیگر عمیات اطلاعات مفیدی را درمورد درخت برمیگرداند.
درج
گرهها در درخت دودویی میتوانند بین دو گره دیگر و یا بعد از گره خارجی درج شوند. در درخت دودویی گره درج شده به عنوان فرزند مشخص میشود. 
گرههای خارجی
گره خارجی اضافه شده گره $A$ است،برای اضافه کردن یک گره بعد از گره $A$ ، گره $A$ گره جدید را به عنوان فرزند مشخص خود میکند و گره جدید گره $A$ را به عنوان گره والد تعیین میکند.
گرههای داخلی
درج در «گرههای داخلی» پیچیدهتر از گرههای خارجی است.فرض میکنیم که $A$ گرۀ داخلی و $B$ فرزند گرۀ $A$ باشد.(اگر درج در قسمت فرزند راست باشد، آنگاه $B$ فرزند سمت راست $A$ است،برای درج فرزند سمت چپ هم همینطور است.) $A$ فرزند جدید را مشخص میکند و گرۀ جدید $A$ را که والدین آن است مشخص میکند.
حذف
حذف فرآیندی است که یک گره را از درخت حذف میکند.فقط میتوان گرههای خاصی را در درخت دودویی به وضوح حذف کرد.

گرۀ بدون فرزند یا دارای یک فرزند
فرض کنید گرهای که میخواهیم حذف کنیم گرۀ $A$ باشد. اگر گره بدون فرزند باشد (گرۀ خارجی) ، آنگاه فرزند والدین گرۀ $A$ تهی میشود. اگر دارای یک فرزند باشد ، آنگاه فرزند $A$ را به والدین گرۀ $A$ متصل میکنیم درنتیجه والدین فرزند $A$ والدین گرۀ $A$ میشود.
گره با دو فرزند
در یک درخت دودویی نمیتوان گره ای که دارای دو فرزند است را به وضوح حذف کرد. اگر چه، در درخت دودویی ( شامل درخت جستجوی دودویی ) این گرهها قابل حذف هستند، ولی با ترمیم ساختمان درخت همراه است.
پیمایش
پیمایشهای پسوندی ، میانوندی و پیشوندی پیمایشهایی هستند که به وسیلۀ آنها میتوان همۀ گرهها زیردرخت چپ ، راست و ریشه را به طور بازگشتی ملاقات کرد.
پیمایش عمق نخستین
در پیمایش عمق نخستین، همیشه قصد ما ملاقات دورترین گرۀ ممکن از گرۀ ریشه است، ولی با این آگاهی که آن گره باید فرزند گرهای باشد که در حال حاضر ملاقات شده است. برعکس در جستجوی عمق نخستین گرافها ، احتیاجی بهبخاطر سپردن گرههایی که قبلاً ملاقات شدهاند نیست، زیرا یک درخت نمیتواند دارای دور باشد. پیمایش پیشوندی یک مورد خاص آن است.
پیمایش عرض نخستین
پیمایش عرض نخستین در مقایسه با عمق نخستین در این است که در این پیمایش همیشه هدف ما ملاقات نزدیکترین گرۀ ملاقات نشده به ریشه است.
در یک درخت دودویی کامل، اندیس عرض گره 1) را میتوان به عنوان دستور العمل پیماش از ریشه مورد استفاده قرار داد. با شروع از بیت d-1 از چپ به راست می خوانیم، که $d$ در آن همان فاصلۀ گره تا ریشه است 2) و در سؤال ، گره نباید خود ریشه باشد (d>0). هنگامی که اندیس عرضی گره بیت d-1 باشد، دارای بیت ارزش $0$و$1$ است یعنی در هر مرحله به طور مرتب چپ یا راست را میپوشاند. فرایند پی در پی با چک کردن بیت بعدی ادامه مییابد تا دیگر بیتی موجود نباشد. سمت راست ترین بیت نشاندهندۀ پیمایش نهایی والدین گرۀ مورد نظر تا خود گره است.

