فهرست مندرجات
مرتب سازی ادغامی
تعریف
مرتب سازی ادغامی نوعی مرتب سازی مقایسهای از مرتبهی زمانی $O(nlogn)$ میباشد که یک نمونه از روش تقسیم و حل میباشد و در بیشتر پیادهسازیها پایدار بوده و ترتیب ورودیهای مساوی را درخروجی حفظ میکند.
الگوریتم
ایدهی الگوریتم این است که با تقسیم مسئله به دو زیر مسئلهی کوچکتر از مرتب بودن دو لیست کوچکتر برای بهدست آوردن لیست حاصل از ادغام آنها استفاده میکند. میتوان الگوریتم مرتب سازی ادغامی را در چند مرحله به صورت کلی بررسی کرد:
1- اگر اندازهی لیست 0 یا 1 بود آن لیست به صورت مرتب شده است در غیر این صورت
2-آن را به دولیست که اندازهی آنها یا باهم برابر است یا 1 واحد فرق دارد تقسیم میکنیم
3-به صورت بازگشتی هر یک از دو لیست را مرتب میکنیم
4-دو لیست مرتب شده را باهم ادغام میکنیم و لیست را مرتب میکنیم
4.1- برای ادغام 2 تا اشارهگر برای اول هر دولیست میگیریم و در هر مرحله اعداد متناظر 2 اشارهگر را با هم مقایسه میکنیم و هر کدام را که کوچکتر بود را در یک آرایهی دیگر مینویسیم واشارهگر متناظرآن را یک واحد جلو میبریم
4.2- در آخر هم اشارهگری که به پایان زیر لیست خود نرسیده را تا آخر زیر لیست آن جلو میبریم و اعداد متنظر آن را در آرایهی کمکی میریزیم
4.3-در آخر هم اعداد آرایهی کمکی را در آرایهی اصلی کپی میکنیم.(ادغام 2 لیست به اندازههای aو b از $O(a+b)$ میباشد چون دو اشارهگر در مجموع a+b گام جلو میآیند )
ابتدا روند الگوریتم راروی توسط یک نمونه نشان میدهیم
آرایهی ۵،۲،۴،۷،۱،۳،۲،۶ را در نظر بگیرید
ابتدا این آرایه را نصف میکنیم پس دو آرایه به طول ۴ بهدست میآید، که برابر است با (۵،۲،۴،۷) و(۱،۳،۲،۶) سپس این روال را تا جایی ادامه میدهیم که که طول آرایههایمان برابر یک شود؛ که برابر است با: (۶)(۲)(۳)(۱)(۷)(۴)(۲)(۵) حال به صورت زیر آنها را با هم ادغام میکنیم تا به آرایه اصلیمان برسیم.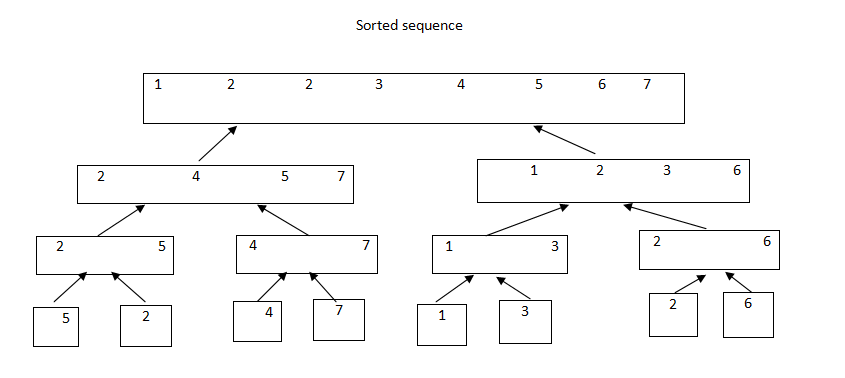
پیچیدگی الگوریتم
در مرتب کردن n تا عنصر مرتبسازی ادغام در حالت میانگین و بدترین حالت دارای زمان اجرای $θ(nlogn)$ میباشد. اگر زمان اجرای مرتبسازی ادغام برای یک لیست به طول 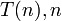 باشد بنابراین رابطهی بازگشتی
باشد بنابراین رابطهی بازگشتی 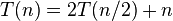 از تعریف الگوریتم پیروی میکند. در این الگوریتم هر دفعه لیست را به دو زیرلیست تقسیم میکنیم و در هر مرحله n تا گام برای ادغام کردن لازم میباشد.
از تعریف الگوریتم پیروی میکند. در این الگوریتم هر دفعه لیست را به دو زیرلیست تقسیم میکنیم و در هر مرحله n تا گام برای ادغام کردن لازم میباشد.
پیادهسازی اولیه
- merge_Sort.cpp
#include <iostream> using namespace std; const int maxn=65537+100; int a[maxn]; int temp[maxn]; int l,m,k; long long res=0; void merge(int left,int mid,int right){ l=left,m=mid+1,k=left-1; while(l<=mid && m<=right){ k+=1; if(a[l]>a[m]){ temp[k]=a[m]; m++; } else{ temp[k]=a[l]; l++; } } if(l>mid) for(int i=0;i<=right-m;i++) temp[k+i+1]=a[m+i]; if(m>right) for(int i=0;i<=mid-l;i++) temp[k+i+1]=a[l+i]; for(int i=left;i<=right;i++) a[i]=temp[i]; } void mergesort(int left,int right){ int mid; if(left==right) return; if(left!=right){ mid=(left+right)/2; mergesort(left,mid); mergesort(mid+1,right); merge(left,mid,right); } } int main() { int n; cin>>n; for(int i=1;i<=n;i++) cin>>a[i]; mergesort(1,n); for(int i=1;i<=n;i++) cout<<a[i]<<endl; return 0; }
کابردها
مثال: http://acm.sgu.ru/problem.php?contest=0&problem=180
پاسخ
- inversions.cpp
#include <iostream> using namespace std; const int maxn=65537+100; int a[maxn]; int temp[maxn]; int l,m,k; long long res=0; void merge(int left,int mid,int right) { l=left,m=mid+1,k=left-1; while(l<=mid && m<=right) { k+=1; if(a[l]>a[m]) { res+=(mid-l+1); temp[k]=a[m]; m++; } else { temp[k]=a[l]; l++; } } if(l>mid) for(int i=0;i<=right-m;i++) temp[k+i+1]=a[m+i]; if(m>right) for(int i=0;i<=mid-l;i++) temp[k+i+1]=a[l+i]; for(int i=left;i<=right;i++) a[i]=temp[i]; } void mergesort(int left,int right) { int mid; if(left==right) return; if(left!=right) { mid=(left+right)/2; mergesort(left,mid); mergesort(mid+1,right); merge(left,mid,right); } } int main() { int n; cin>>n; for(int i=1;i<=n;i++) cin>>a[i]; mergesort(1,n); cout<<res<<endl; return 0; }

